Giáo án Dạy thêm Hình học Lớp 9 - Chủ đề 11: Góc cơ đỉnh bên trong đường tròn. Góc cơ đỉnh bên ngoài đường tròn

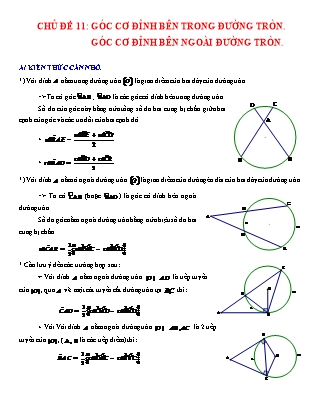
CHỦ ĐỀ 11: GÓC CƠ ĐỈNH BÊN TRONG ĐƯỜNG TRÒN.
 GÓC CƠ ĐỈNH BÊN NGOÀI ĐƯỜNG TRÒN.
A/ KIẾN THỨC CẦN NHỚ. 
*) Với đỉnh nằm trong đường tròn là giao điểm của hai dây của đường tròn 
=> Ta có góc ; là các góc có đỉnh bên trong đường tròn. 
Số đo của góc này bằng nửa tổng số đo hai cung bị chắn giữa hai cạnh của góc và các tia đối của hai cạnh đó. 
+ . 
+ 
*) Với đỉnh nằm ở ngoài đường tròn là giao điểm của đường éo dài của hai dây của đường tròn 
	=> Ta có (hoặc ) là góc có đỉnh bên ngoài đường tròn.
Số đo góc nằm ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.
* Cần lưu ý đến các trường hợp sau:
+ Với đỉnh nằm ngoài đường tròn . là tiếp tuyến của , qua vẽ một cát tuyến cắt đường tròn tại thì:
+ Với Với đỉnh nằm ngoài đường tròn . là 2 tiếp tuyến của , ( là các tiếp điểm) thì: 
B/ BÀI TẬP VẬN DỤNG.
I. BÀI TẬP MẪU.
Bài 1: Cho ΔABC nhọn nội tiếp đường tròn (O). Vẽ phân giác trong AD của góc A (D ≠ (O)). Lấy điểm E thuộc cung nhỏ AC. Nối BE cắt AD và AC lần lượt tại I và tại K, nối DE cắt AC tại J. Chứng minh rằng: 
a) ∠BID = ∠AJE . 
b) AI.JK = IK.EJ. 
Hướng dẫn
a) Ta có ∠BID là góc có đỉnh nằm bên trong đường tròn (O) chắn hai cung BD và cung AE
∠AJE là góc có đỉnh nằm bên trong đường tròn (O) chắn hai cung CD và AE
Mà AD là phân giác của góc A nên 
Suy ra ∠BID = ∠ẠJE
b) Xét ΔAIK và ΔEJK có:
+) ∠AKI = ∠EKJ (đối đỉnh)
+) ∠IAK = ∠KEJ (hai góc nội tiếp chắn hai cung bằng nhau BD và cung CD )
Do đó ΔAIK ∼ ΔEJK (g.g)
=> AI/EJ = IK/JK => AI.JK = IK.EJ
Bài 2: Cho hai đường tròn (O) và (O’) cắt nhau tại 2 điểm A, B sao cho O ≠ (O'). Lấy điểm M thuộc đường tròn (O’), M ở trong đường tròn (O). Tia AM và BM cắt đường tròn (O) lần lượt tại C và D. Chứng minh rằng:
a) (Cung nhỏ của đường tròn (O))
b) Tứ giác ABCD là hình thang cân.
Hướng dẫn
a) Vì ∠AMB là góc có đỉnh nằm bên trong đường tròn (O) chắn hai cung AB và CD nên: 
Mặt khác: ∠AMB = ∠AOB (hai góc nội tiếp (O’) cùng chắn cung AB lớn)
∠AOB = sđ (góc ở tâm đường tròn (O)).
b) Trong đường tròn (O):
 ; 
Mà => 
Vì hai góc này ở vị trí so le trong,
suy ra AD // BC 	(1)
Theo câu a), ta có: ∠ADC = ∠DAB (2 góc chắn 2 cung bằng nhau)	(2)
Từ (1) và (2) suy ra tứ giác ABCD là hình thang cân.
Bài 3: Cho ΔABC đều nội tiếp đường tròn (O). Điểm I chuyển động trên cung nhỏ BC. AB cắt CI tại M, AC cắt BI tại N. Chứng minh rằng:
a) BC2 = BM.CN
b) ∠AIN có số đo không đổi.
Hướng dẫn
a) Vì ΔABC đều nên: 
Ta có: ∠ANB là góc có đỉnh ngoài đường tròn (O) nên:
Lại có: (góc nội tiếp (O) chắn cung BI)
Suy ra ∠ANB = ∠BCI 	(1)
Tương tự ta có: ∠AMC = ∠CBI 	(2)
Từ (1) và (2) suy ra: ΔBCM ∼ ΔCNB (g-g) => BC/NC = BM/BC => BC2 = BM.NC
b) Ta có: ∠AIB = ∠ACB = 60o
=> ∠AIN = 180o - ∠AIB = 120o không đổi
Bài 4: Qua điểm A nằm ngoài đường tròn (O) vẽ tiếp tuyến AB và cát tuyến ACD với đường tròn (C nằm giữa A và D). Vẽ dây BM vuông góc với tia phân giác của ∠BAC, BM cắt CD tại I. Chứng minh rằng:
a) BM là tia phân giác của
b) MD2 = MI.MB
Hướng dẫn
Giả sử tia phân giác của ∠BAC cắt BC tại E, cắt BD tại E và cắt đường tròn (O) tại K.
a) Ta có:
Mà ∠A1 = ∠A2 (gt)
=> ó 
⇔ ∠BEF = ∠BFE
=> ΔBEF cân tại B.
Mà BM là đường cao của ΔBEF
Suy ra BM là tia phân giác của ∠CBD
b) Vì BM là phân giác của ∠CBD
Do đó: ΔMDI ∼ ΔMBD (g.g)
=> MD2 = MI.MB
II/ LUYỆN TẬP.
Bài 1: Cho đường tròn (O) và dây cung AB, CD cắt nhau tại điểm E nằm ngoài đường tròn. Đường thẳng kẻ từ E song song với AD cắt BC tại F. Kẻ tiếp tuyến FG với đường tròn (O). Chứng minh rằng:
a) 
b) ΔFEC ∼ ΔFBE, từ đó suy ra EF2 = FB.FC
Bài 2: Cho hai đường tròn (O) và (O’) ở ngoài nhau. Đường thẳng OO’ cắt (O) và (O’) lần lượt lại các điểm A, B, C, D. Kẻ tiếp tuyến chung ngoài EF của hai đường tròn (E ≠ (O), F ≠ (O')) . Gọi M là giao điểm của AE và DF, N là giao điểm của EB và DC. Chứng minh rằng:
a) Tứ giác MENF là hình chữ nhật.
b) MN ⊥ AD
c) ME.MA = MF.MD.
Bài 3: Trên đường tròn (O; R) đặt liên tiếp các dây cung: AB = BC = CD < R. AB cắt CD tại E. Tiếp tuyến tại B và D với đường tròn (O) cắt nhau tại F. Chứng minh rằng:
a) ΔEBC ∼ ΔFBD
b) ΔEBF ∼ ΔCBD
c) BC // EF.
Bài 4: Cho tứ giác ABCD có A, B, C, D nằm trên đường tròn (O); AB và CD cắt nhau tại M; AD và BC cắt nhau tại N.
a) Tính số đo các góc của tứ giác ABCD nếu ∠AMD = 30o và ∠BND = 40o .
b) Hai phân giác của góc M và góc N cắt nhau tại I. Chứng minh rằng IM ⊥ IN
Bài 5: Cho đường tròn tâm O và điểm M ngoài đường tròn đó . Từ M kẻ tiếp tuyến MA và cát tuyến MBC đến đường tròn ( B nằm giữa M và C ) . Phân giác của góc cắt BC ở D , cắt đường tròn ở E . Chứng minh : 
a) MD = MA 
b) AD . AE = AC . AB 
Bài 6: Cho tam giác ABC nội tiếp đường tròn tâm O . Các tia phân giác của các góc A và B cắt nhau ở I và cắt đường tròn theo thứ tự ở D và E . Chứng minh rằng : 
a) DBDI là tam giác cân .
b) DE là đường trung trực của IC . 
c) IF // BC ( F là giao điểm của DE và AC ).
Bài 7: Cho đường tròn tâm O và điểm S ở ngoài đường tròn . Từ S kẻ hai tiếp tuyến SA và SD và cát tuyến SBC tới đường tròn ( B ở giữa S và C ).
a) Phân giác của góc cắt dây cung BC ở M . Chứng minh SA = SM . 
b) AM cắt đường tròn ở E. Gọi G là giao điểm của OE và BS; F là giao điểm của AD với BC . Chứng minh SA2 = SG . SF . 
c) Biết SB = a ; Tính SF khi BC = 
Bài 8: Từ điểm M ở ngoài đường tròn (I) kẻ hai tiếp tuyến ME và MF ( E và F là hai tiếp điểm ) . Kẻ dây EG của đường tròn (I) song song MF. Gọi H là giao điểm của MG với (I) và K là giao điểm của EH với MF . 
 	a) Chứng minh KF2 = KE . KH . 
 	b) Chứng minh K là trung điểm của MF . 
Bài 9: Cho đường tròn (O) đường kính EF và điểm G nằm trên nằm trên đường tròn (O) sao cho EG > GF. Trên tia GF lấy điểm H sao cho GH =GE . Vẽ hình vuông EGHI có đường chéo GI cắt (O) tại K .
a) Chứng minh DKFH cân .
b) Tiếp tuyến tại E với đường tròn (O) cắt FK ở M . Chứng minh ba điểm M , I , H thẳng hàng 
Bài 10: Cho tứ giác ABCD có A, B, C , D nằm trên đường tròn (O) . Các tia AB và DC cắt nhau tại E , các tia CB và DA cắt nhau tại F . Hai phân giác của các góc và cắt nhau tại K . Chứng minh rằng : = 900 . 
Bài 11: Cho tam giác đều ABC nội tiếp đường tròn tâm O . điểm D di chuyển trên cung AC . Gọi E là giao điểm của AC và BD . Chứng minh rằng : 
 	a) 
 	b) Tích AE . BF không đổi .
Bài 12: Trên đường tròn (O) lấy ba điểm A,B và C . Gọi M,N và P theo thứ tự là điểm chính giữa của các cung AB,BC và AC. BP cắt AN tại I , NM cắt AB tại E . Gọi D là giao điểm của AN và BC . Chứng minh rằng : 
a) DBNI cân . 
b) AE.BN = EB.AN . 
c) EI // BC 
d)