Giáo án Dạy thêm Hình học Lớp 9 - Chủ đề 10: Góc tạo bởi tiếp tuyến và dây
1. Định nghĩa
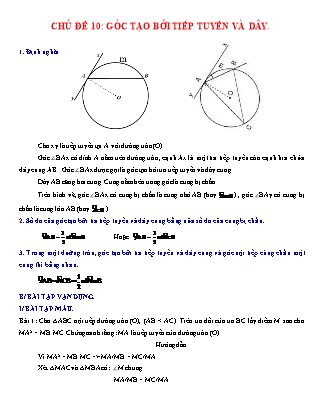
Cho xy là tiếp tuyến tại A với đường tròn (O).
Góc ∠BAx có đỉnh A nằm trên đường tròn, cạnh Ax là một tia tiếp tuyến còn cạnh kia chứa dây cung AB. Góc ∠BAx được gọi là góc tạo bởi tia tiếp tuyến và dây cung.
Dây AB căng hai cung. Cung nằm bên trong góc là cung bị chắn.
Trên hình vẽ, góc ∠BAx có cung bị chắn là cung nhỏ AB (hay ) , góc ∠BAy có cung bị chắn là cung lớn AB (hay )
2. Số đo của góc tạo bởi tia tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn.
Hoặc
Bạn đang xem tài liệu "Giáo án Dạy thêm Hình học Lớp 9 - Chủ đề 10: Góc tạo bởi tiếp tuyến và dây", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
CHỦ ĐỀ 10: GÓC TẠO BỞI TIẾP TUYẾN VÀ DÂY. 1. Định nghĩa Cho xy là tiếp tuyến tại A với đường tròn (O). Góc ∠BAx có đỉnh A nằm trên đường tròn, cạnh Ax là một tia tiếp tuyến còn cạnh kia chứa dây cung AB. Góc ∠BAx được gọi là góc tạo bởi tia tiếp tuyến và dây cung. Dây AB căng hai cung. Cung nằm bên trong góc là cung bị chắn. Trên hình vẽ, góc ∠BAx có cung bị chắn là cung nhỏ AB (hay ) , góc ∠BAy có cung bị chắn là cung lớn AB (hay ) 2. Số đo của góc tạo bởi tia tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn. Hoặc 3. Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau. B/ BÀI TẬP VẬN DỤNG. I/ BÀI TẬP MẪU. Bài 1: Cho ΔABC nội tiếp đường tròn (O), (AB < AC). Trên tia đối của tia BC lấy điểm M sao cho MA2 = MB.MC. Chứng minh rằng: MA là tiếp tuyến của đường tròn (O). Hướng dẫn Vì MA2 = MB.MC => MA/MB = MC/MA Xét ΔMAC và ΔMBA có: ∠M chung MA/MB = MC/MA => ΔMAC ∼ ΔMBA (c.g.c) => ∠MAB = ∠MCA (1) Kẻ đường kính AD của (O) . Ta có ∠ACB = ∠ADB (hai góc nội tiếp cùng chắn cung AB ) Mà ∠MAB = ∠MCA (chứng minh trên) Suy ra ∠MAB = ∠ADB (2) Lại có ∠ABD = 90o (góc nội tiếp chắn nửa đường tròn) => ∠BAD + ∠BDA = 90o (3) Từ (2) và (3) suy ra ∠BAD + ∠MAB = 90o hay ∠MAO = 90o => OA ⊥ MA Do A ∈ (O) => MA là tiếp tuyến của (O). Bài 2: Từ điểm M nằm ngoài đường tròn (O) vẽ hai tiếp tuyến MA, MB với (O) tại A và B. Qua A vẽ đường thẳng song song với MB cắt đường tròn tại C. Nối C với M cắt đường tròn (O) tại D. Nối A với D cắt MB tại E. Chứng minh rằng: a) ΔABE ∼ ΔBDE; ΔMEA ∼ ΔDEM. b) E là trung điểm của MB. Hướng dẫn a) Chứng minh ΔABE ∼ ΔBDE; ΔMEA ∼ ΔDEM. Xét ΔABE và ΔBDE có: ∠E chung ∠BAE = ∠DBE (góc nội tiếp và góc giữa tia tiếp tuy ến và dây cung cùng chắn cung BD ) => ΔABE ∼ ΔBDE (g.g) Vì AC // MB nên ∠ACM = ∠CMB (so le trong) Mà ∠ACM = ∠MAE (góc nội tiếp và góc giữa tia tiếp tuyến và dây cung cùng chắn cung AD ) Suy ra: ∠CMB = ∠MAE Xét ΔMEA và ΔDEM có: ∠E chung ∠MAE = ∠CMD (chứng minh trên) => ΔMEA ∼ ΔDEM (g.g) b) Chứng minh E là trung điểm của MB Theo chứng minh a) ta có: ΔABE ∼ ΔBDE => AE/BE = BE/DE => EB2 = AE.DE ΔMEA ∼ ΔDEM => ME/DE = EA/EM => ME2 = DE.EA Do đó EB2 = EM2 hay EB = EM. Vậy E là trung điểm của MB. Bài 3: Cho điểm C thuộc nửa đường tròn (O) đường kính AB. Từ điểm D thuộc đọan AO kẻ đường thẳng vuông góc với AO cắt AC và BC lần lượt lại E và F. Tiếp tuyến C với nửa đường tròn cắt EF tại M và cắt AB tại N. a) Chứng minh M là trung điểm của EF. b) Tìm vị trí của điểm C trên đường tròn (O) sao cho ΔACN cân tại C. Hướng dẫn a) Chứng minh M là trung điểm của EF Ta có ∠MCA = 1/2 sđ (góc giữa tiếp tuyến và dây cung chắn cung AC) (1) Lại có ∠MEC = ∠AED = 90o - ∠EAD = 90o - 1/2 sđ = 1/2 sđ (2) Từ (1) và (2) suy ra ∠MCE = ∠MEC Vậy ΔMEC cân tại M, suy ra MC = ME. Chứng minh tương tự ta có MC = MF. Suy ra ME = MF hay M là trung điểm của EF. b) Tìm vị trí của điểm C trên đường tròn (O) sao cho ΔACN cân tại C. ΔACN cân tại C khi và chỉ khi ∠CAN = ∠CNA Vì MN là tiếp tuyến với (O) tại C nên OC ⊥ MN => ∠CNA = 90o - ∠COB = 90o - 2.∠CAN Do đó: ∠CAN = ∠CNA ⇔ ∠CAN = 90o - 2.∠CAN ⇔ 3∠CAN = 90o => ∠CAN = 30o => Sđ = 60o Vậy ΔACN cân tại C khi C nằm trên nửa đường tròn (O) sao cho SđBC = 60o . Bài 4: Cho nửa đường tròn (O) đường kính AB = 2R. Gọi M là một điểm thay đổi trên tiếp tuyến Bx của (O). Nối AM cắt (O) tại N. Gọi I là trung điểm của AN. a) Chứng minh: ΔAIO ∼ ΔBMN ; ΔOBM ∼ ΔINB b) Tìm vị trí của điểm M trên tia Bx để diện tích ΔAIO có giá trị lớn nhất. Hướng dẫn a) Chứng minh: ΔAIO ∼ ΔBMN ; ΔOBM ∼ ΔINB Vì I là trung điểm của AN => OI ⊥ AN => ∠AIO = ∠ANB = 90o Do Bx là tiếp tuyến với (O) tại B => ∠NBM = ∠IAO = 1/2 sđ => ΔAIO ∼ ΔBMN (g.g) Vì ∠OIM = ∠OBM = 90o => các điểm B, O, I, M cùng thuộc đường tròn đường kính MO suy ra ∠BOM = ∠BIN Xét ΔOBM và ΔINB có: ∠OBM = ∠INB ∠BOM = ∠BIN => ΔOBM ∼ ΔINB (g.g) b) Tìm vị trí của điểm M trên tia Bx để diện tích ΔAIO có giá trị lớn nhất Kẻ IH ⊥ AO ta có: SΔAIO = 1/2 AO.IH Vì AO không đổi nên SΔAIO lớn nhất ⇔ IH lớn nhất. Nhận thấy: Khi M chuyển động trên tia Bx thì I chạy trên nửa đường tròn đường kính AO. Do đó IH lớn nhất khi IH là bán kính của đường tròn => ΔAIO vuông cân tại I nên ∠IAH = 45o. => ΔABM vuông cân tại B nên BM = BA = 2R Vậy khi M thuộc Bx sao cho BM = 2R thì SΔAIO lớn nhất. Bài 5: Cho đường tròn (O; R) và dây AB, gọi I là trung điểm của dây AB. Trên tia dối của tia BA lấy điểm M. Kẻ hai tiếp tuyến MC, MD với đường tròn, (C,D ≠ (O)) . a) Chứng minh rằng: Năm điểm O, I, C, M, D cùng nằm trên một đường tròn. b) Gọi N là giao điểm của tia OM với (O). Chứng minh rằng N là tâm đường tròn nội tiếp . Hướng dẫn a) Chứng minh rằng: Năm điểm O, I, C, M, D cùng nằm trên một đường tròn. Vì MC, MD là các tiếp tuyến tại C, D với đường tròn (O) => ∠OCM = ∠ODM = 90o (1) Mặt khác I là trung điểm của dây AB nên OI ⊥ AB hay ∠OIM = 90o (2) Từ (1), (2) suy ra 5 điểm M, C, D, O, I cùng thuộc đường tròn đường kính OM. b) Chứng minh rằng N là tâm đường tròn nội tiếp Vì MC, MD là các tiếp tuyến của (O) => MO là phân giác của ∠CMD (3) Mà: ∠DCN = ∠NCM = 1/2 sđ Suy ra CN là phân giác của ∠DCM (4) Từ (3) và (4) suy ra N là giao điểm các đường phân giác trong của ΔCMD => N là tâm đường tròn nội tiếp ΔCMD II/ LUYỆN TẬP. Bài 1 : Từ một điểm M cố định ở bên ngoài đường tròn (O) , kẻ một tiếp tuyến MT ( T là tiếp điểm ) và một cát tuyến MAB của đường tròn đó . a) Chứng minh : MT2 = MA . MB b) Trường hợp cát tuyến MAB đi qua tâm O . Cho MT = 20 cm , và cát tuyến dài nhất cùng xuất phát từ M bằng 50cm. Tính bán kính R của đường tròn (O) . Bài 2: Cho nửa đường tròn (O) đường kính AB. Trên tia đối của tia AB lấy một điểm M . Vẽ tiếp tuyến MC với nửa đường tròn . Gọi H là hình chiếu của C trên AB . a) Chứng minh rằng CA là tia phân giác của góc MCH . b) Giả sử MA =a, MC = 2a . Tính AB và CH theo a . Bài 3: Cho đường tròn (O1) tiếp xúc trong với đường tròn (O) tại A . Đường kính AB của đường tròn (O) cắt đường tròn (O1) tại điểm thứ hai C khác A . Từ B vẽ tiếp tuyến BP với đường tròn (O1) cắt đường tròn (O) tại Q . Chứng minh AP là phân giác của góc Bài 4: Cho hai đường tròn tâm O , O1 tiếp xúc ngoài nhau tại A . Trên đường tròn (O) lấy hai điểm phân biệt B , C khác A. Các đường thẳng BA , CA cắt đường tròn (O1) tại P và Q . Chứng minh PQ // BC . Bài 5: Cho tam giác ABC nội tiếp đường tròn (O) và ( AB < AC ) . Đường tròn (I) đi qua B và C , tiếp xúc với AB tại B cắt đường thẳng AC tại D . Chứng minh rằng : OA ^ BD . Bài 6 : Cho nửa đường tròn (O) đường kính AB= 2R, dây AC và tia tiếp tuyến Bx nằm trên cùng nửa mặt phẳng bờ AB chứa nửa đường tròn . Tia phân giác của góc CAB cắt dây BC tại F , cắt nửa đường tròn tại H , cắt Bx ở D. a) Chứng minh FB = DB và HF = HD b) Gọi M là giao điểm của AC và Bx . Chứng minh AC . AM = AH . AD c) Tính tích AF .AH + BF.BC theo bán kính R của đường tròn (O) Bài 7 : Cho tam giác ABC nội tiếp đường tròn tâm O . Phân giác góc BAC cắt đường tròn (O) ở M . Tiếp tuyến kẻ từ M với đường tròn cắt các tia AB và AC lần lượt ở D và E . Chứng minh : a) BC // DE b) DAMB và DMCE dồng dạng ,DAMC và DMDB đồng dạng. c) Nếu AC = CE thì MA2 = MD . ME Bài 8 : Cho hai đường tròn (O) và (O1) ở ngoài nhau . Đường nối tâm OO1 cắt các đường tròn (O) và (O1) tại các điểm A , B , C , D theo thứ tự trên đường thẳng . Kẻ tiếp tuyến tuyến chung ngoài EF ( E Î (O) , F Î (O1) ) . Gọi M là giao điểm của AE và DF , N là giao điểm của EB và FC . Chứng minh rằng: a) Tứ giác MENF là hình chữ nhật . b) MN ^ AD c) ME . MA = MF . MD Bài 9: Cho tam giác ABC vuông ở A nội tiếp đường tròn tâm O đường kính 5cm . Tiếp tuyến với đường tròn tại C cắt tia phân giác của góc ABC tại K . BK cắt AC tại D và BD = 4cm . Tính độ dài BK .
Tài liệu đính kèm:
 giao_an_day_them_hinh_hoc_lop_9_chu_de_10_goc_tao_boi_tiep_t.docx
giao_an_day_them_hinh_hoc_lop_9_chu_de_10_goc_tao_boi_tiep_t.docx



