Giáo án Dạy thêm Hình học Lớp 9 - Chương III, Bài 5: Góc có đỉnh bên trong đường tròn. Góc có đỉnh bên ngoài đường tròn
I.Tóm tắt lý thuyết
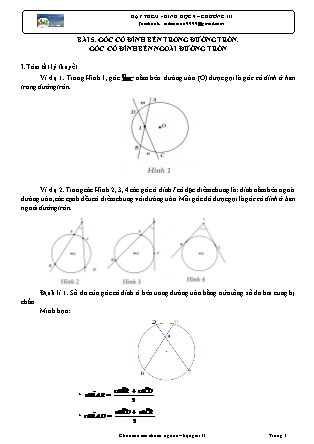
Ví dụ 1. Trong Hình 1, góc nằm bên đường tròn (O) được gọi là góc có đỉnh ở hên trong đường tròn.
Ví dụ 2. Trong các Hình 2, 3, 4 các góc ở đỉnh I có đặc điểm chung là: đỉnh nằm bên ngoài đường tròn, các cạnh đều có điếm chung với đường tròn. Mỗi góc đó được gọi là góc có đỉnh ở bên ngoài đường tròn.
Định lí 1. Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
Bạn đang xem tài liệu "Giáo án Dạy thêm Hình học Lớp 9 - Chương III, Bài 5: Góc có đỉnh bên trong đường tròn. Góc có đỉnh bên ngoài đường tròn", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
BÀI 5. GÓC CÓ ĐỈNH BÊN TRONG ĐƯỜNG TRÒN. GÓC CÓ ĐỈNH BÊN NGOÀI ĐƯỜNG TRÒN I.Tóm tắt lý thuyết Ví dụ 1. Trong Hình 1, góc nằm bên đường tròn (O) được gọi là góc có đỉnh ở hên trong đường tròn. Ví dụ 2. Trong các Hình 2, 3, 4 các góc ở đỉnh I có đặc điểm chung là: đỉnh nằm bên ngoài đường tròn, các cạnh đều có điếm chung với đường tròn. Mỗi góc đó được gọi là góc có đỉnh ở bên ngoài đường tròn. Định lí 1. Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn. Minh họa: + . + Định lí 2. Số đo của góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn. Minh họa: Lưu ý: + Với đỉnh nằm ngoài đường tròn . là tiếp tuyến của , qua vẽ một cát tuyến cắt đường tròn tại thì: + Với Với đỉnh nằm ngoài đường tròn . là 2 tiếp tuyến của , ( là các tiếp điểm) thì: II. Các dạng bài tập Dạng 1. Chứng minh hai góc hoặc hai đoạn thẳng bằng nhau Phương pháp giải: Sử dụng hai định lý về số đo của góc có đỉnh bên trong đường tròn, góc có đỉnh bên ngoài đường tròn. Bài 1: Từ điểm M nằm ngoài đường tròn (O), kẻ tiếp tuyến MC tại C và cát tuyên MAB (A nằm giữa M và B) và A,B,C Î (O). Gọi D là điểm chính giữa của cung AB không chứa C, CD cắt AB tại I. Chứng minh: a) ; b) MI = MC. Hướng Dẫn: a) b) Sử dụng kết quả câu a). Bài 2: Cho đường tròn (O) và một điểm P nằm ngoài (O). Kẻ cát tuyến PAB và tiếp tuyến PT với A,B,T Î (O). Đường phân giác của góc ATB cắt AB tại D. Chứng minh PT = PD. Hướng Dẫn: HS tự làm. Bài 3: Cho tam giác ABC nội tiếp đường tròn (O). Các tia phân giác của các góc B và C cắt nhau tại I và cắt (O) lần lượt tại D và E. Dây DE cắt các cạnh AB và AC lần lượt tại M và N. Chứng minh: a) Các tam giác AMN, EAI và DAI là những tam giác cân; b) Tứ giác AMIN là hình thoi. Hướng Dẫn: a) Suy ra DAMN cân tại A. Kéo dài AI cắt đường tròn (o) tại K. Chứng minh tương tự, ta có DAIE và DDIA lần lượt cân tại E và D. b) Xét DAMN cân tại A có AI là phân giác. Suy ra AI ^ MN tại F và MF = FN. Tương tự với DEAI cân tại E, ta có: AF = IF. Vậy tứ giác AMIN là hình hình hành. Mà AI ^ MN Þ ĐPCM. Bài 4: Cho tam giác ABC ngoại tiếp đường tròn (I). Các tia AI, BI, CI cắt đường tròn ngoại tiếp tam giác ABC tại D, E, F. Dây EF cắt AB, AC lần lượt tại M và N. Chứng minh: a) DI = DB; b) AM = AN; Hướng Dẫn: HS tự làm. Dạng 2. Chứng minh hai đường thẳng song song hoặc vuông góc. Chứng minh các đẳng thức cho trước Phương pháp giải: Áp dụng hai định lý về số đo của góc có đỉnh bên trong đường tròn, góc có đỉnh bên ngoài đường tròn để có được các góc bằng nhau, cạnh bằng nhau. Từ đó, ta suy điều cần chứng minh. Bài 1: Từ điểm P ở ngoài (O), vẽ tiếp tuyến PA với đ/tròn và cát tuyến PBC với P, B,C Î (O). a) Biết PC = 25cm; PB = 49cm. Đường kính (O) là 50cm. Tính PO. b) Đường phân giác trong của góc A cắt PB ở I và cắt (O) ở D. Chứng minh DB là tiếp tuyến của đường tròn ngoại tiếp DAIB. Hướng Dẫn: a) Chứng minh được PA2 = PC.PB và PA2 = PO2 = OA2 Þ tính được PO. b) Chứng minh được Þ ĐPCM Bài 2: Cho (O) có hai đường kính AB và CD vuông góc với nhau. Trên đường kính AB lấy điểm E sao cho AE = . Vẽ dây CF đi qua E. Tiếp tuyên của đường tròn tại F cắt CD tại M, vẽ dây Aỉ cắt CD tại N. Chứng minh: a) Tia CF là tia phân giác của góc BCD; b) MF và AC song song; c) MN, OD, OM là độ dài 3 cạnh của một tam giác vuông. Hướng Dẫn: a) Học sinh tự chứng minh. b) Chứng minh . c) Chứng minh: cân tại Mặt khác: OD = OF = R. Ta có MF là tiếp tuyến nên DOFM vuông Þ ĐPCM. Bài 3: Cho tam giác ABC phân giác AD. Vẽ đường tròn (O) đi qua A, D và tiếp xúc với BC tại D. Đường tròn này cắt AB, AC lần lượt tại E và F. Chứng minh: a) EF song song BC; b) AD2 = AE.AC; c) AE.AC = AB.AF. Hướng Dẫn: a) HS tự chứng minh. b) (g-g) Þ AD2 = AE.AC c) Tương tự: Þ AD2 = AB.AF Þ ĐPCM. Bài 4: Cho tam giác ABC nội tiếp đường tròn tâm O. Các tia phân giác của các góc A và B cắt nhau ở I và cắt đường tròn theo thứ tự ở D và E. Chứng minh: a) Tam giác BDI là tam giác cân; b) DE là đường trung trực của IC; c) IF và BC song song, trong đó F là giao điểm của DE và AC. Hướng Dẫn: a) sđ cân ở D. b) Chứng minh tương tự: DIEC cân tại E, DDIC cân tại D. Þ EI = EC và DI = DC Þ DE là trung trực của CI. c) F Î DE nên FI = FC III. Bài tập tự luyện Bài 1: Từ điểm P nằm ngoài đường tròn (O), kẻ hai cát tuyến PAB và PCD (A nằm giữa P và B, C nằm giữa P và D), các đường thẳng AD và BC cắt nhau tại Q. a) Cho biết = 60° và = 80°. Tính góc b) Chứng minh PA.PB = PC.PD. Hướng Dẫn: a) Ta có: (sđ - sđ), (sđ + sđ) = sđ = 1400 b) HS tự chứng minh Bài 2: Từ một điểm A bên ngoài (O), vẽ tiếp tuyến AB và cát tuyến ACD. Tia phân giác của góc cắt BC và BD lần lượt tại M và N. Vẽ dây BF vuông góc với MN, cắt MN tại H, cắt CD tại E. Chứng minh: a) Tam giác BMN cân; b) FD2 = FE.FB. Hướng Dẫn: a) HS tự chứng minh cân ở B. b) Bài 3: Cho tam giác đều MNP nội tiếp đường tròn tâm (O). Điểm D di chuyển trên . Gọi E là giao điểm của MP và ND, gọi F là giao điểm của MD và NP. Chứng minh Hướng Dẫn: HS tự chứng minh Bài 4: Trên đường tròn (O) lấy ba điểm A, B và C. Gọi M, N và P theo thứ tự là điểm chính giữa cua các cung AB, BC và AC. BP cắt AN tại I, NM cắt AB tại E. Gọi D là giao điểm của AN và BC. Chứng minh: a) Tam giác BNI cân; b) AE.BN = EB.AN; c) EI song song BC; d) Hướng Dẫn: a) HS tự chưng minh b) M chính giữa là phân giác (tính chất đường phân giác) Þ BN.AE = NA.BE c) Chứng tinh tương tự 4B d) Chứng minh Þ ĐPCM Bài 5: Từ điểm M nằm bên ngoài đường tròn (O), vẽ tiếp tuyến MA và cát tuyến MCB với A,B,C Î (O). Phân giác góc cắt BC tại D, cắt (O) tại N. Chứng minh: a) MA = MD; b) Cho cát tuyến MCB quay quanh M và luôn cắt đ/tròn. Chứng minh MB.MC không đổi. c) NB2 = NA.ND. Hướng Dẫn: HS tự chứng minh Bài 6: Tam giác MNP nội tiếp đường tròn tâm (O), các điểm I, K, H là điểm chính giữa của các cung MN, NP, PM. Gọi J là giao điểm của IK và MN, G là giao điểm của HK và MP. Chứng minh JG song song với NP. Hướng Dẫn: KG là đường phân giác của (1) KJ là đường phân giác của (2) Chứng minh được: KN = KP (3) Từ (1); (2); (3) Þ ĐPCM Bài 7: Trên đường tròn cho các điểm theo thứ tự đó. Gọi lần lượt là điểm chính giữa của các cung và . Chứng minh các đường thẳng và vuông góc với nhau. Hướng Dẫn: Gọi là giao điểm của và ; theo thứ tự là số đo của các cung . Khi đó . Xét góc là góc có đỉnh nằm trong đường tròn . Ta có . Nghĩa là (đpcm). Bài 8: Cho bốn điểm theo thứ tự đó nằm trên đường tròn tâm đường kính ( và nằm về cùng một phía so với ). Gọi và theo thứ tự là hình chiếu vuông góc của trên đường thẳng . Tia cắt tia tại . Biết rằng . a) Tính số đo . b) Trên cung nhỏ lấy điểm . Gọi giao điểm của với lần lượt là và . Tìm giá trị lớn nhất của khi di động trên cung nhỏ . Hướng Dẫn: a). Kẻ , Ta thấy là đường trung bình của hình thang , Suy ra . Từ đó tam giác đều, Suy ra . Ta thấy có đỉnh nằm ngoài đường tròn Nên . b) Ta thấy Suy ra (không đổi) Do đó lớn nhất khi và chỉ khi nhỏ nhất. Theo trên, không đổi Nên nhỏ nhất khi . Vậy giá trị lớn nhất của bằng . Bài 9: Trong tam giác , đường phân giác của cắt cạnh tại . Giả sử là đường tròn tiếp xúc với tại và đi qua điểm . Gọi là giao điểm thứ hai của và , là giao điểm thứ hai của và , là giao điểm của và . a) Chứng minh rằng . b) Chứng minh hệ thức . Hướng Dẫn: a). Gọi là giao điểm thứ hai của với đường tròn . Do là phân giác của Nên . Ta có (đpcm). b) Từ kết quả câu a, Ta thấy . Từ đó (g.g), Suy ra Hay (đpcm). Bài 10: Trên đường tròn ta lấy các điểm theo thứ tự đó. a) Chứng minh rằng nếu các đường thẳng là các đường phân giác trong của tam giác thì chúng là các đường cao của . b) CHứng minh rằng nếu các đường thẳng là các đường cao của tam giác thì chúng là đường phân giác trong của tam giác . Hướng Dẫn: a)Ta chứng minh . Thật vậy, gọi là giao điểm của và , khi đó: (đpcm). Chứng minh tương tự ta cũng có . b)Gọi là giao điểm của và . Ta có (1) Lại có (2). Vì , Nên từ (1) và (2) suy ra . Tức là chứa đường phân giác của . Chứng minh tương tự, ta cũng thu được chứa đường phân giác của , chứa đường phân giác của . Bài 11: Cho ΔABC nhọn nội tiếp đường tròn (O). Vẽ phân giác trong AD của góc A (D ≠ (O)). Lấy điểm E thuộc cung nhỏ AC. Nối BE cắt AD và AC lần lượt tại I và tại K, nối DE cắt AC tại J. Chứng minh rằng: a) ∠BID = ∠AJE . b) AI.JK = IK.EJ. Hướng Dẫn: a) Ta có ∠BID là góc có đỉnh nằm bên trong đường tròn (O) chắn hai cung BD và cung AE ∠AJE là góc có đỉnh nằm bên trong đường tròn (O) chắn hai cung CD và AE Mà AD là phân giác của góc A nên Suy ra ∠BID = ∠ẠJE b) Xét ΔAIK và ΔEJK có: +) ∠AKI = ∠EKJ (đối đỉnh) +) ∠IAK = ∠KEJ (hai góc nội tiếp chắn hai cung bằng nhau BD và cung CD ) Do đó ΔAIK ∼ ΔEJK (g.g) => AI/EJ = IK/JK => AI.JK = IK.EJ Bài 12:Cho hai đường tròn (O) và (O’) cắt nhau tại 2 điểm A, B sao cho O ≠ (O'). Lấy điểm M thuộc đường tròn (O’), M ở trong đường tròn (O). Tia AM và BM cắt đường tròn (O) lần lượt tại C và D. Chứng minh rằng: a) (Cung nhỏ của đường tròn (O)) b) Tứ giác ABCD là hình thang cân. Hướng dẫn: a) Vì ∠AMB là góc có đỉnh nằm bên trong đường tròn (O) chắn hai cung AB và CD nên: Mặt khác: ∠AMB = ∠AOB (hai góc nội tiếp (O’) cùng chắn cung AB lớn) ∠AOB = sđ (góc ở tâm đường tròn (O)). b) Trong đường tròn (O): ; Mà => Vì hai góc này ở vị trí so le trong, suy ra AD // BC (1) Theo câu a), ta có: ∠ADC = ∠DAB (2 góc chắn 2 cung bằng nhau) (2) Từ (1) và (2) suy ra tứ giác ABCD là hình thang cân. Bài 13: Cho ΔABC đều nội tiếp đường tròn (O). Điểm I chuyển động trên cung nhỏ BC. AB cắt CI tại M, AC cắt BI tại N. Chứng minh rằng: a) BC2 = BM.CN b) ∠AIN có số đo không đổi. Hướng Dẫn: a) Vì ΔABC đều nên: Ta có: ∠ANB là góc có đỉnh ngoài đường tròn (O) nên: Lại có: (góc nội tiếp (O) chắn cung BI) Suy ra ∠ANB = ∠BCI (1) Tương tự ta có: ∠AMC = ∠CBI (2) Từ (1) và (2) suy ra: ΔBCM ∼ ΔCNB (g-g) => BC/NC = BM/BC => BC2 = BM.NC b) Ta có: ∠AIB = ∠ACB = 60o => ∠AIN = 180o - ∠AIB = 120o không đổi Bài 14: Qua điểm A nằm ngoài đường tròn (O) vẽ tiếp tuyến AB và cát tuyến ACD với đường tròn (C nằm giữa A và D). Vẽ dây BM vuông góc với tia phân giác của ∠BAC, BM cắt CD tại I. Chứng minh rằng: a) BM là tia phân giác của b) MD2 = MI.MB Hướng Dẫn: Giả sử tia phân giác của ∠BAC cắt BC tại E, cắt BD tại E và cắt đường tròn (O) tại K. a) Ta có: Mà ∠A1 = ∠A2 (gt) => ó ⇔ ∠BEF = ∠BFE => ΔBEF cân tại B. Mà BM là đường cao của ΔBEF Suy ra BM là tia phân giác của ∠CBD b) Vì BM là phân giác của ∠CBD Do đó: ΔMDI ∼ ΔMBD (g.g) => MD2 = MI.MB Bài 15: Cho tam giác ABC nội tiếp trong đường tròn (O). Trên các cung nhỏ AB và AC lần lượt lấy các điểm I và K sao cho . Dây IK cắt các cạnh AB, AC lần lượt tại D và E. a) Chứng minh rằng . b) Tam giác ABC phải có thêm điều kiện gì thì tứ giác DECB là hình thang cân. Hướng Dẫn: a) b) . Bài 16: Cho đường tròn (O) và một dây AB. Vẽ đường kính CD vuông góc với AB (D thuộc cung nhỏ AB). Trên cung nhỏ BC lấy một điểm N. Các đường thẳng CN và DN lần lượt cắt đường thẳng AB tại E và F. Tiếp tuyến của đường tròn (O) tại N cắt đường thẳng AB tại I. Chứng minh rằng: a) Các tam giác INE và INF là các tam giác cân. b) . Hướng Dẫn: a) b) Þ đpcm. Bài 17: Cho tam giác ABC nội tiếp đường tròn (O). Các tia phân giác của góc B và góc C cắt nhau tại I và cắt đường tròn (O) lần lượt tại D và E. Dây DE cắt các cạnh AB và AC lần lượt tại M và N. Chứng minh rằng: a) Tam giác AMN là tam giác cân. b) Các tam giác EAI và DAI là những tam giác cân. c) Tứ giác AMIN là hình thoi. Hướng Dẫn: a) Þ b) Þ DA = DI c) Chứng minh NI // AM, MI // AN, AM = AN Þ đpcm. Bài 18: Từ một điểm M ở bên ngoài đường tròn (O), ta vẽ hai tiếp tuyến MB, MC. Vẽ đường kính BD. Hai đường thẳng CD và MB cắt nhau tại A. Chứng minh rằng M là trung điểm của AB. Hướng Dẫn: Þ MA = MC = MB. Bài 19: Từ một điểm A ở bên ngoài đường tròn (O), ta vẽ hai cát tuyến ABC và ADE (B nằm giữa A và C; D nằm giữa A và E). Cho biết , . Chứng minh CD ^ BE. Hướng Dẫn: . Gọi H = CD Ç BE Þ . Bài 20: Cho 4 điểm A, B, C và D theo thứ tự trên đường tròn (O) sao cho số đo các cung như sau: , . Gọi I là giao điểm của AC và BD. M là giao điểm của DA và CB kéo dài. Tính các góc CID và AMB. Hướng Dẫn: Bài 21: Cho đường tròn (O). Từ một điểm M ở ngoài (O), ta vẽ các cát tuyến MAC và MBD sao cho . Gọi E là giao điểm của AD và BC. Biết góc , tính số đo các cung AB và CD. Hướng Dẫn: Bài 22: Cho đường tròn (O) và một điểm M ở ngoài (O). Vẽ tiếp tuyến MA và cát tuyến MBC đi qua O (B nằm giữa M và C). Đường tròn đường kính MB cắt MA tại E. Chứng minh: với , và là các cung trong góc AMC. Hướng Dẫn:
Tài liệu đính kèm:
 giao_an_day_them_hinh_hoc_lop_9_chuong_iii_bai_5_goc_co_dinh.doc
giao_an_day_them_hinh_hoc_lop_9_chuong_iii_bai_5_goc_co_dinh.doc



