Bài giảng Hình học Lớp 9 - Bài 6: Tính chất của hai tiếp tuyến cắt nhau

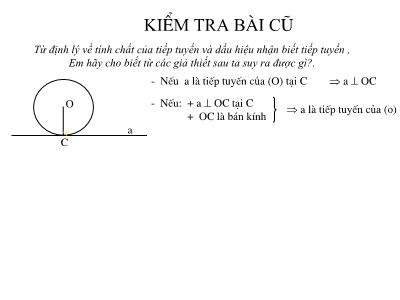
KiÓm tra bµi còTừ định lý về tính chất của tiếp tuyến và dấu hiệu nhận biết tiếp tuyến ,Em hãy cho biết từ các giả thiết sau ta suy ra được gì?.OCa- NÕu a lµ tiÕp tuyÕn cña (O) t¹i C - NÕu: + a  OC t¹i C + OC lµ b¸n kÝnh a lµ tiÕp tuyÕn cña (o) a  OCTRANG TRÍ HÌNH TRÒNThước phân giácVới " thước phân giác ", ta có thể tìm được tâm của một vật hình tròn ?? 1: Cho hình vẽ: Tiếp tuyến tại B và C của đường tròn (O) cắt nhau tại A . Hãy dự đoán những yếu tố nào bằng nhau ?§6. TÍNH CHẤT CỦA HAI TIẾP TUYẾN CẮT NHAUACBOABCO1212 OAB = OAC (c.h+cgv) Suy ra: AB = AC.  Â1 = Â2.  Ô1 = Ô2. A cách đều hai tiếp điểm B và C. AO là tia phân giác của BÂC. OA là tia phân giác của BÔC.Dựa vào ? 1 em hãy điền vào ô trống để được một định lý .OABC1212 Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì: Điểm đó hai tiếp điểm. Tia kẻ từ ...đi qua .là ......................của góc tạo bởi hai tiếp tuyến.Tia kẻ từ đi qua .. là ...................của góc tạo bởi hai bán kính đi qua tiếp điểm.§6. TÍNH CHẤT CỦA HAI TIẾP TUYẾN CẮT NHAUcách đềuđiểm đó tâmtia phân giáctâmđiểm đó tia phân giácĐịnh lý 1/ Tính chất hai tiếp tuyến cắt nhau: a. 450 b. 600 c. 300 Bài tập: Cho hình vẽ, HB và HC là các tiếp tuyến của đường tròn (O). 	Biết CHB = 600 .Hãy chọn đáp án đúng:	12121.Số đo góc O1 là :2. Số đo góc COB là:	a. 600	b. 900	c. 1200 HBC có gì đặc biệt ? HBC là tam giác đều. OHBCGiao điểm hai đường kẻ là tâm hình trònThước phân giác. OOĐường tròn ngoại tiếp tam giác là 	đường tròn như thế nào?Cách xác định tâm đường tròn 	ngoại tiếp tam giác?Bài toán 2. Cho ABC. Gọi I là giao điểm của các đường phân giác các góc trong của tam giác; D, E, F theo thứ tự là chân các đường vuông góc kẻ từ I đến các cạnh BC, AC, AB. Chứng minh rằng ba điểm D, E, F nằm trên cùng một đường tròn tâm I.EFDICBA2. Đường tròn nội tiếp tam giácEFDICBA2. Đường tròn nội tiếp tam giácGTKL ABCI là giao điểm các đường phân giácID  BC, IE  AC, IF  ABID = IE = IF Giải I nằm trên đường phân giác góc C => ID = IEI nằm trên đường phân giác góc A => IE = IF ID = IE = IF D, E, F nằm trên cùng một đường tròn (I)EFDICBAĐường tròn nội tiếp tam giácTam giác ngoại tiếp đường trònĐịnh nghĩa: Đường tròn tiếp xúc với ba cạnh của một tam giác gọi là đường tròn nội tiếp tam giác, còn tam giác gọi là ngoại tiếp đường tròn.Cách xác định tâm :Tâm của đường tròn nội tiếp tam giác là giao điểm của các đường phân giác các góc trong của tam giác.2. Đường tròn nội tiếp tam giácABCIDABCIO..ABCOIABKDEFxy3. Đ­ưêng trßn bµng tiÕp tam gi¸c:Bài toán 3:Cho tam giác ABC, K là giao điểm các đường phân giác của hai góc ngoài tại B và C. D, E, F theo thứ tự là chân các đường vuông góc kẻ từ K đến các đường thẳng BC, AC, AB. Chứng minh rằng D, E , F nằm trên cùng một đường tròn có tâm K.CABCKDEFxy ABCFBK = DBK, DCK = ECKKD  BC, KE  Cy, KF  BxGTKLKD = KE = KFVì K thuộc tia phân giác của góc CBx nên: KD = KFVì K thuộc tia phân giác của góc BCy nên: KD = KEDo đó KD = KE = KFVậy D, E, F cùng thuộc đường tròn (K)Giải3. Đ­ưêng trßn bµng tiÕp tam gi¸c:ABCKDEFxyĐịnh nghĩa: Đường tròn tiếp xúc với một cạnh của một tam giác và các phần kéo dài của hai cạnh kia gọi là đường tròn bàng tiếp tam giác.Cách xác định tâm đường tròn bàng tiếp tam giác trong góc A: + Là giao điểm hai đường phân giác các góc ngoài tại B và C + Hoặc là giao điểm của đường phân giác góc A và đường phân giác góc ngoài tại B (hoặc C). Đường tròn (K) bàng tiếp trong góc A của ABCĐường tròn bàng tiếp tam giác3. Đường trßn bµng tiÕp tam gi¸c:Một tam giác có mấy đường tròn bàng tiếp ?Ba đường tròn (O1), (O2), (O3) là các đường tròn bàng tiếp tam giác ABCO1O2BCAO3Được bạn Bên cạnh bắt tayChúc may mắn lần sauĐược + 5đ1 tràng vỗ tay Được cộng 5đMất quyền12756843Hộp quà bí mậtBACKC©u sè 1Hộp quà bí mậtChọn đáp án đúng:Đường tròn nội tiếp tam giác là đường tròn......... với ba cạnh của tam giác.	a. tiếp xúc.	b. cắt 	c. không giaoC©u sè 2Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì:Điểm đó cách đều tâm và các tiếp điểm.Điểm đó cách đều hai tiếp điểm.Điểm đó cách đều các bán kính.Chọn đáp án đúng.Hộp quà bí mậtC©u sè 3Tâm đường tròn nội tiếp tam giác là giao điểm của:	a. Hai đường phân giác trong tam giác.	b. Hai đường phân giác ngoài tam giác.	c. Hai đường trung trực của tam giác.Chọn đáp án đúng.Hộp quà bí mậtÔ May mắn+10đC©u sè 4Hộp quà bí mậtC©u sè 5Hộp quà bí mậtTâm đường tròn bàng tiếp tam giác là giao điểm của:Hai đường phân giác trong tam giác.Hai đường phân giác ngoài của tam giácHai đường cao của tam giác.Chọn đáp án đúng.C©u sè 6Hộp quà bí mậtABCOCho AB và AC là hai tiếp tuyến của đường tròn (O) như hình vẽ.Ta có:a. BAO = CAOb. BAO = BOAc. BOA = AOCChọn đáp án sai.C©u sè 8Hộp quà bí mậtSMNOTiếp tuyến SM và SN của (O) cắt nhau tại S như hình vẽ. Góc có số đo bằng góc SON là :SOMMSONSOC©u sè 8Chúc bạn may mắn lần sauC©u sè 7Hộp quà bí mậtHướng dẫn về nhàHọc thuộc định lí về tính chất hai tiếp tuyến cắt nhau.BTVN: 26, 27 (SGK)Bài tập (hoạt động nhóm 4 người): Hãy nối một câu ở cột A với một câu ở cột B để được khẳng định đúngCột ACột BNối1. Đường tròn nội tiếp tam giác2. Đường tròn bàng tiếp tam giác3.Đường tròn ngoại tiếp tam giác4. T©m ®­êng trßn néi tiÕp tam gi¸c5.T©m ®­êng trßn bµng tiÕp tam gi¸ca - là đường tròn tiếp xúc với ba cạnh của tam giácb - là giao điểm ba đường phân giác trong tam giácc - là đường tròn tiếp xúc với một cạnh của tam giác và phần kéo dài của hai cạnh kia.d - là đường tròn đi qua ba đỉnh của tam giác.e - là giao điểm hai đường phân giác ngoài của tam giác.1- a2 - c3 - d4 - b 5 - eTrß ch¬i: 1§­êng trßn néi tiÕp tam gi¸c lµ ®­êng trßn ............................. cña tam gi¸c.NÕu mét ®­êng th¼ng lµ tiÕp tuyÕn cña mét ®­êng trßn th× nã . víi b¸n kÝnh ®i qua tiÕp ®iÓm. T©m ®­êng trßn ngo¹i tiÕp tam gi¸c lµ giao ®iÓm ba ®­êng cña tam gi¸c.§­êng trßn ngo¹i tiÕp tam gi¸c lµ ®­êng trßn .. cña tam gi¸c.NÕu hai tiÕp tuyÕn cña mét ®­êng trßn c¾t nhau t¹i mét ®iÓm th× ®iÓm ®ã . hai tiÕp ®iÓm.®i qua ba ®ØnhtiÕp xóc víi ba c¹nhvu«ng gãcc¸ch ®Òutrung trùctrung tuyÕnph©n gi¸cChän côm tõ thÝch hîp ë bªn ph¶i ®iÒn vµo chç (...) cho ®óng:T©m ®­êng trßn néi tiÕp tam gi¸c lµ giao ®iÓm ba ®­êng c¸c gãc trong cña tam gi¸c.234561. Đường tròn nội tiếp tam giác2. Đường tròn bàng tiếp tam giác3.Đường tròn ngoại tiếp tam giác4. T©m ®­êng trßn néi tiÕp tam gi¸c5.T©m ®­êng trßn bµng tiÕp tam gi¸c6.Tâm đường tròn ngoại tiếp tam giác.a - là đường tròn tiếp xúc với ba cạnh của tam giácb - là giao điểm ba đường phân giác trong tam giácc - là đường tròn tiếp xúc với một cạnh của tam giác và phần kéo dài của hai cạnh kia.d - là đường tròn đi qua ba đỉnh của tam giác.h- là giao điểm hai đường phân giác ngoài của tam giác.e. là giao điểm của ba đường trung trực của tam giác.g. là giao điểm của ba đường trung tuyến của tam giác