Bài giảng Hình học Lớp 9 - Luyện tập tính chất của hai tiếp tuyến cắt nhau

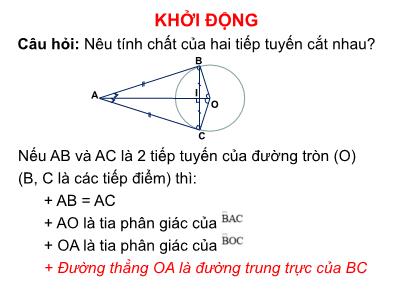
KHỞI ĐỘNGCâu hỏi: Nêu tính chất của hai tiếp tuyến cắt nhau?Nếu AB và AC là 2 tiếp tuyến của đường tròn (O)(B, C là các tiếp điểm) thì: + AB = AC + AO là tia phân giác của + OA là tia phân giác của + Đường thẳng OA là đường trung trực của BCIBAOCCách 1Ta có AB và AC là hai tiếp tuyến của (O) => AB = AC (t/c) => cân tại A Do AO là tia phân giác của góc BAC (t/c) => AO là đường trung trực của BC Cách 2 Ta có: AB và AC là hai tiếp tuyến của (O) => AB = AC (t/c) Lại có: OB = OC (bán kính (O)) => AO là đường trung trực của BCIBAOCNếu AB và AC là 2 tiếp tuyến của đường tròn (O)(B, C là các tiếp điểm) thì: + AB = AC + AO là tia phân giác của + OA là tia phân giác của + Đường thẳng OA là đường trung trực của BCIBAOCLUYỆN TẬPBài 1. Cho đường tròn (O;R), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn (B,C là các tiếp điểm). Gọi I và E là giao điểm của AO với BC và đường tròn (E nằm giữa A và O). Chứng minh: a) OI. OA = OB2 b) E là tâm đường tròn nội tiếp AOIEBCChứng minh: OI. OA = OB2 Giải: Có: AB OB (t/c tiếp tuyến) vuông tại B Mặt khác: OB = OC = R AB = AC (t/c tiếp tuyến) OA là đường trung trực của BC OA BC tại I Xét vuông tại B, có đường cao BI OI. OA = OB2 (hệ thức lượng)AOIEBCb) Chứng minh: E là tâm đường tròn nội tiếp E là tâm đường tròn nội tiếp tam giác ABCBE là phân giác AE là phân giác (Tính chất) cân tại OOE = OB = R AOIEBCb) Chứng minh: E là tâm đường tròn nội tiếpGiải: Có: AB là tiếp tuyến của (O)	 AB OB (t/c) AB = AC (t/c tiếp tuyến) OB = OC = R OA là đường trung trực của BC BC OA tại I cân tại O Từ (1), (2) và (3) 	 BE là phân giác của Có AE là phân giác của (t/c tiếp tuyến) E là tâm đường tròn nội tiếp Bài 2. Cho nửa đường tròn (O;R), có đường kính AB. Kẻ hai tia Ax và By vuông góc với AB (Ax, By và nửa đường tròn (O) thuộc cùng một nửa mặt phẳng bờ chứa AB). Trên nửa đường tròn lấy điểm M (M khác A và B), qua M kẻ tiếp tuyến với nửa đường tròn, nó cắt Ax và By theo thứ tự tại C và D.Chứng minh: AC + BD = CD Tích AC.BD không đổi khi M di chuyển trên nửa đường tròn.a) Có: Ax vuông góc với AB tại A By vuông góc với AB tại B AB là đường kính của (O) Ax và By là 2 tiếp tuyến của (O) AC = CM (t/c tiếp tuyến) BD = MD (t/c tiếp tuyến) AC + BD = CM + MD AC + BD = CD (đpcm)b) Do AC và MC là 2 tiếp tuyến của (O) OC là tia phân giác của BD và DM là hai tiếp tuyến của (O) OD là tia phân giác của Có và là 2 góc kề bù (đpcm)c) Chứng minh: Tích AC.BD không đổi khi M di chuyển trên nửa đường tròn. AC. BD không đổi CM. DM không đổi OM2 không đổic) Chứng minh: Tích AC.BD không đổi khi M di chuyển trên nửa đường tròn.Giải: Có: AC = CM (t/c tiếp tuyến) BD = DM (t/c tiếp tuyến) AC. BD = CM. DMDo CD là tiếp tuyến của (O) tại M (t/c) Xét vuông tại O, đường cao OM CM. DM = OM2 (hệ thức lượng) AC. BD = OM2 = R2 AC. BD không đổiPHIẾU THẢO LUẬN NHÓMCho hình vẽ.Có Ax, By, CD là các tiếp tuyếncủa nửa đường tròn (O).Tứ giác MEOF là hình gì? . . .2) EF và AB có quan hệ gì? .. ..EFMK // AC // BDK là trung điểm của MHAB là tiếp tuyến của đường tròn đường kính CDHKMNPKHIA. IO = IE. IFAF. IE = AE. IFOI. OA = OM. OQ4) OI. OA = OH. OK5) KN là tiếp tuyến của (O)Liên hệ thực tế