Đề cương ôn tập học kỳ I môn Toán Lớp 9 - Năm học 2020-2021 - Trường THCS Nguyễn Gia Thiếu
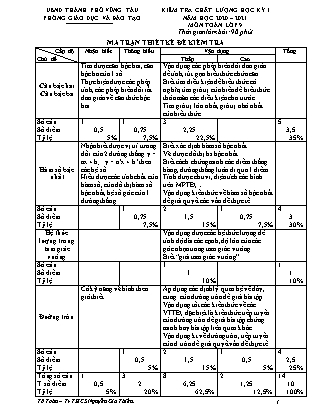
Bài 11. Cho biểu thức M = ; với a 0 và a 1
a) Rút gọn biểu thức M b) Tính giá trị M biết a =
c) Tìm a để M < 0="">
Bài 12. Cho biểu thức: A = ; với x > 0 và x ≠ 1
a) Rút gọn biểu thức A; b) Tính giá trị của biểu thức A tại
Bài 13. Cho biểu thức: B =
a) Tìm TXĐ rồi rút gọn biểu thức B; b) Tính giá trị của B với x = 3;
c) Tìm giá trị của x để
Bài 14. Cho biểu thức C =
a) Tìm điều kiện để biểu thức C có nghĩa;
b) Rút gọn biểu thức C; c) Với giá trị nào của x thì C <>
Bài 15. Cho biểu thức: D =
a) Tìm TXĐ rồi rút gọn biểu thức D; b) Tìm x Z để D nhận giá trị nguyên;
c) Tìm giá trị lớn nhất của D; d) Chứng minh rằng: nếu 0 < x="">< 1="" thì="" d=""> 0
Bạn đang xem tài liệu "Đề cương ôn tập học kỳ I môn Toán Lớp 9 - Năm học 2020-2021 - Trường THCS Nguyễn Gia Thiếu", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
UBND THÀNH PHỐ VŨNG TÀU PHÒNG GIÁO DỤC VÀ ĐÀO TẠO KIỂM TRA CHẤT LƯỢNG HỌC KỲ I NĂM HỌC 2020 – 2021 MÔN TOÁN LỚP 9 Thời gian làm bài: 90 phút MA TRẬN THIẾT KẾ ĐỀ KIỂM TRA Cấp độ Chủ đề Nhận biết Thông hiểu Vận dụng Tổng Thấp Cao Căn bậc hai Căn bậc ba Tìm được căn bậc hai, căn bậc ba của 1 số. Thực hiện được các phép tính, các phép biến đổi rất đơn giản về căn thức bậc hai. Vận dụng các phép biến đổi đơn giản để tính, rút gọn biểu thức chứa căn. Biết tìm điều kiện để biểu thức có nghĩa, tìm giá trị của biến để biểu thức thỏa mãn các điều kiện cho trước. Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức. Số câu Số điểm Tỷ lệ 1 0,5 5% 1 0,75 7,5% 3 2,25 22,5% 5 3,5 35% Hàm số bậc nhất Nhận biết được vị trí tương đối của 2 đường thẳng y = ax + b; y = a’x + b’ theo các hệ số. Hiểu được các tính chất của hàm số, của đồ thị hàm số bậc nhất, hệ số góc của 1 đường thẳng... Biết xác định hàm số bậc nhất. Vẽ được đồ thị hs bậc nhất. Biết cách chứng minh các điểm thẳng hàng, đường thẳng luôn đi qua 1 điểm. Tính được chu vi, diện tích các hình trên MPTĐ, Vận dụng kiến thức về hàm số bậc nhất để giải quyết các vấn đề thực tế. Số câu Số điểm Tỷ lệ 1 0,75 7,5% 2 1,5 15% 1 0,75 7,5% 4 3 30% Hệ thức lượng trong tam giác vuông Vận dụng được các hệ thức lượng để tính độ dài các cạnh, độ lớn của các góc nhọn trong tam giác vuông. Biết “giải tam giác vuông”. Số câu Số điểm Tỷ lệ 1 1 10% 1 1 10% Đường tròn Có kỹ năng vẽ hình theo giả thiết. Áp dụng các định lý quan hệ về dây, cung của đường tròn để giải bài tập. Vận dụng tốt các kiến thức về các VTTĐ, đặc biệt là kiến thức tiếp tuyến của đường tròn để giải bài tập chứng minh hay bài tập liên quan khác. Vận dụng kt về đường tròn, tiếp tuyến của đ tròn để giải quyết vấn đề thực tế. Số câu Số điểm Tỷ lệ 1 0,5 5% 2 1,5 15% 1 0,5 5% 4 2,5 25% Tổng số câu T số điểm Tỷ lệ 1 0,5 5% 3 2 20% 8 6,25 62,5% 2 1,25 12,5% 14 10 100% ỦY BAN NHÂN DÂN TP VŨNG TÀU TRƯỜNG THCS NGUYỄN GIA THIỀU ĐỀ CƯƠNG ÔN TẬP HỌC KÌ I - TOÁN 9 NĂM HỌC 2020-2021 ĐẠI SỐ CHƯƠNG I: CĂN BẬN HAI – CĂN BẬC BA DẠNG 1: TÌM ĐIỀU KIỆN XÁC ĐỊNH CỦA BIỂU THỨC. Bài 1: Với giá trị nào của x thì các biểu thức sau đây xác định: a) b) c) d) e) f) g) h) DẠNG 2: TÍNH GIÁ TRỊ CỦA BIỂU THỨC CHỨA CĂN: Bài 2: Tính (Rút gọn): a) b) c) Bài 3: Tính (Rút gọn): a) b) c) d) Bài 4: Tính (Rút gọn): a) b) c) d) Bài 5: Tính (Rút gọn): a) b) DẠNG 3: TÌM GIÁ TRỊ CỦA x: Bài 6: Tìm x, biết: a) b) c) d) Bài 7: Tìm x, biết: a) b) c) = 0 d) DẠNG 4: RÚT GỌN BIỂU THỨC CHỨA CĂN THỨC BẬC HAI Bài 8. Chứng minh rằng biểu thức sau không phụ thuộc vào biến: Với x ≥ 0; y ≥ 0; x ≠ y Với x ≥ 0; y ≥ 0; x ≠ y Bài 9. Chứng minh đẳng thức: a) ; với b) ; (với a ≥ 0) Bài 10. Rút gọn biểu thức: (với a ≥ 0; b ≥ 0; a ≠ b) ; (với a 0; a1) (với a ≥ 0; b ≥ 0; a ≠ b) (với a > 0; a1) DẠNG 5: BÀI TẬP TỔNG HỢP VỀ CĂN THỨC Bài 11. Cho biểu thức M = ; với a 0 và a 1 a) Rút gọn biểu thức M b) Tính giá trị M biết a = c) Tìm a để M < 0 . Bài 12. Cho biểu thức: A = ; với x > 0 và x ≠ 1 a) Rút gọn biểu thức A; b) Tính giá trị của biểu thức A tại Bài 13. Cho biểu thức: B = a) Tìm TXĐ rồi rút gọn biểu thức B; b) Tính giá trị của B với x = 3; c) Tìm giá trị của x để Bài 14. Cho biểu thức C = a) Tìm điều kiện để biểu thức C có nghĩa; b) Rút gọn biểu thức C; c) Với giá trị nào của x thì C < -1 Bài 15. Cho biểu thức: D = a) Tìm TXĐ rồi rút gọn biểu thức D; b) Tìm x Î Z để D nhận giá trị nguyên; c) Tìm giá trị lớn nhất của D; d) Chứng minh rằng: nếu 0 0 ------ oOo ------ CHƯƠNG II: HÀM SỐ BẬC NHẤT DẠNG 1: XÁC ĐỊNH TÍNH BIẾN THIÊN CỦA HÀM SỐ Bài 1. Các hàm số sau đây đồng biến hay nghịch biến trên R? Vì sao? a) b) Bài 2. Với giá trị nào của m thì hàm số đồng biến ? nghịch biến? a) y = (m + 4)x – m + 6 ; m ≠ - 4 b) y = (1 - 4m)x + m – 2 ; Bài 3: Cho hàm số bậc nhất y = (2 – a)x + a . Biết đồ thị hàm số đi qua điểm M(3;1), hàm số đồng biến hay nghịch biến trên R? Vì sao? Bài 4: Cho hàm số bậc nhất y = (1– 3m)x + m + 3 đi qua N(1; –1), hàm số đồng biến hay nghịch biến ? Vì sao? DẠNG 2: TÌM HỆ SỐ a CỦA HÀM SỐ y = ax + b . Bài 1. Cho hàm số y = ax + 2. Tìm a, biết khi x = 3 thì hàm số có giá trị y = 7. Bài 2. Biết rằng đồ thị hàm số y = (m – 2)x + 5 đi qua điểm A(– 1; 3). Tìm m. Bài 3. Cho hàm số y = (m + 1)x + 2. Tìm m, biết đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng – 4. Bài 4. Cho hàm số bậc nhất y = ax +3. Tìm hệ số a, biết đồ thị hàm số cắt đường thẳng y = 3x – 1 tại điểm có hoành độ bằng 2. Bài 5. Biết đồ thị hàm số y = (k – 3)x – 4 cắt đường thẳng y = –3x + 2 tại điểm có tung độ bằng 5. Tìm tham số k. Bài 6. Cho hàm số y = (5 – m)x + 9. Tìm m, biết đồ thị hàm số song song với đường thẳng y = – 2x + 5. DẠNG 3: TÌM HỆ SỐ b CỦA HÀM SỐ y = ax + b Bài 1. Biết rằng với x = 4 thì hàm số y = 3x + b có giá trị 11. Tìm b. Bài 2. Cho hàm số y = x + m – 1. Xác định m, biết đồ thị của hàm số đã cho cắt trục tung tại điểm có tung độ bằng – 3. Bài 3. Cho hàm số y = x + b. Xác định hệ số b, biết đồ thị của hàm số đã cho cắt trục hoành tại điểm có hoành độ bằng – 10. Bài 4. Cho hàm số y = –3x + b. Xác định b, biết đồ thị của hàm số này đi qua điểm A(1;5). Bài 5. Cho hàm số y = 3x + 1 – m. Tìm hệ số m, biết đồ thị hàm số cắt đường thẳng y = 2020x + 4 tại một điểm trên trục tung. Bài 6. Cho hàm số y = – 3x + b. Tìm b, biết đồ thị hàm số cắt đường thẳng y = 2x – 4 tại một điểm trên trục hoành. Bài 7. Cho hàm số y = x + b. Xác định b, biết đồ thị hàm số cắt đường thẳng y = – 3x + 1 tại một điểm có hoành độ bằng 4. Bài 8. Biết đồ thị hàm số y = x + b cắt đường thẳng y = 2x + 3 tại một điểm có tung độ bằng 2. Xác định hệ số b. DẠNG 4: TÌM HỆ SỐ a VÀ b CỦA HÀM SỐ y = ax + b Bài 1. Cho hàm số y = ax + b. Tìm a và b, biết đồ thị của hàm số cắt trục tung tại điểm có tung độ – 2 và cắt trục hoành tại điểm có hoành độ bằng – 3. Bài 2. Cho hàm số y = ax + b. Tìm a và b, biết đồ thị của hàm số song song với đường thẳng y = x + 1 và đi qua điểm A. Bài 3. Cho hàm số y = ax + b. Tìm a và b, biết đồ thị của hàm số song song với đường thẳng y = – 4x + 2020 và cắt đường thẳng y = 2021x – 3 tại một điểm trên trục tung. DẠNG 5: ĐỒ THỊ HÀM SỐ y = ax + b Bài 1. Cho hàm số y = 2x – 1 có đồ thị (d). a) Vẽ đường thẳng (d) trên mặt phẳng tọa độ. b) Xác định hàm số y = ax+ b biết đồ thị hàm số này song song với đường thẳng (d) và đi qua điểm (-3;-2). Bài 2. Cho hàm số y = –2x+ b có đồ thị là (d). a) Xác định b và vẽ đồ thị hàm số, biết đồ thị của nó đi qua điểm A(1; 2). b) Viết phương trình đường thẳng (d’), biết (d’) song song với đường thẳng (d) và cắt trục hoành tại điểm có hoành độ bằng 3. Bài 3. Cho hàm số a) Vẽ đồ thị hàm số. b) Gọi A và B là giao điểm của đồ thị hàm số với trục Ox, Oy. Tính diện tích tam giác OAB. Bài 4. Cho hàm số y = ax–2 (a ≠ 0), có đồ thị là đường thẳng (d). a) Xác định a, biết (d) song song với đường thẳng y =1–3x. Vẽ đường thẳng (d). b) Tìm tọa độ giao điểm của đường thẳng (d) và đường thẳng (d’): y = x+ 6 Bài 5. Cho hàm số , đồ thị là (d). a) Vẽ đồ thị (d). b) Tính góc tạo bởi (d) với trục Ox (làm tròn đến phút). Bài 6. Xác định hàm số y = ax+ b có đồ thị là đường thẳng (d), biết (d) cắt trục tung tại điểm có tung độ gốc là 2 và có hệ số góc là –2. Vẽ (d). Bài 7. Xác định hàm số y = ax+b biết đồ thị của nó cắt trục tung tại điểm có tung độ bằng 3 và cắt trục hoành tại điểm có hoành độ bằng –2. Vẽ đồ thị hàm số vừa xác định. Bài 8. Xác định hàm số y = ax+ b trong mỗi trường hợp sau, biết đồ thị của hàm số là đường thẳng đi qua gốc tọa độ và: a) đi qua điểm A(3; 2) b) có hệ số góc bằng c) song song với đường thẳng y =11x+2020 Bài 9. Tìm điều kiện của k và m để hai đường thẳng: y = kx + (m-2) và y = (5–k)x+ (4–m) a) Song song ; b) Cắt nhau ; c) Trùng nhau. Bài 10. Cho hai hàm số bậc nhất y = -2x + 5 (d ) và y = 0,5 x (d’) a) Tìm tọa độ điểm M là giao điểm của (d) và (d’) bằng phép tính. b) Tính góc α tạo bởi đường thẳng d với trục hoành Ox (làm tròn kết quả đến phút) *c) Gọi giao điểm của d với trục Oy là A. Tính chu vi và diện tích tam giác MOA. DẠNG 6 : TOÁN CÓ NỘI DUNG THỰC TẾ Bài 1. Một khu vườn hình chữ nhật có kích thước 20m và 35m. Người ta tăng mỗi kích thước của khu vườn thêm x (mét). Gọi P là chu vi của khu vườn sau khi tăng kích thước. Hỏi P có phải là một hàm số bậc nhất của x không? Tại sao? Bài 2. Vừa qua lớp 9A mua 1 tờ giấy roky và 8 cây bút mầu để làm báo tường chào mừng ngày Nhà giáo Việt Nam 20/11. Biết rằng số tiền mua một tờ giấy roky là 10 000 đồng và giá tiền mua bút mầu là x đồng/cây. Em hãy viết hàm số biểu diễn chi phí y (đồng) mà lớp 9A đã dùng mua giấy và bút mầu? Bài 3. Gia đình bạn An đi Vũng Tàu bằng taxi. Hãng taxi quy định giá mở cửa là 10 000 đồng. Nếu giá mỗi km là x đồng, hãy viết hàm số y biểu diễn số tiền gia đình bạn An phải trả khi đi 12 km? ------ oOo ------ HÌNH HỌC CHƯƠNG I: - HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG - TỶ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN DẠNG 1: ÁP DỤNG HỆ THỨC LƯỢNG ĐỂ TÍNH ĐỘ DÀI DOẠN THẲNG Bài 1. Cho các hình vẽ sau. Hãy tính độ dài các đoạn thẳng còn lại. 5 12 x y a h c b 4 9 a h c b x 8 a 6 (hình 1) (hình 2) (hình 3) c 15 x y 17 h 5 b x y a 3 c b x y 10 4 Bài 2. Cho ∆ABC vuông tại A, đường cao AH. Tính diện tích ∆ABC, biết AH = 12cm, BH = 9cm. Bài 3. Cho ∆ABC biết BC = 7,5cm, AC = 4,5cm, AB = 6cm. a) ∆ABC là tam giác gì? Tính đường cao AH của ∆ABC. b) Tính độ dài các cạnh BH, HC. Bài 4. Cho ∆ABC vuông tại A. Biết , BC = 26cm. Tính AB, AC, HB, HC. Bài 5. Cho ∆ABC vuông tại A, AB = 12cm, AC = 16cm, phân giác AD, đường cao AH. Tính HD, HB, HC. DẠNG 2: TÍNH TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN Bài 1. ChoABC vuông tại A. Biết AB = 7cm, AC = 21cm. Tính các tỉ số lượng giác của góc B và C. Bài 2. ChoABC vuông tại A. Biết sinB = 0,6. Tính các tỉ số lượng giác của góc C. Bài 3. Cho biết cosα = 0,4. Hãy tìm sinα, tanα, cotα Bài 4. Cho biết tanα + cotα = 3. Tính sinα.cosα DẠNG 3: SO SÁNH, SẮP XẾP CÁC TỈ SỐ LƯỢNG GIÁC Bài 1. Sắp xếp các tỉ số sau theo thứ tự tăng dần: sin300, cos420, cos670, sin380 , sin750 Bài 2. Sắp xếp các tỉ số sau theo thứ tự giảm dần: tan270, cot490, tan800, tan250, cot500 . DẠNG 4: GIẢI TAM GIÁC VUÔNG Giải tam giác ABC vuông tại A, biết: a) AB = 10 cm; góc B bằng 300; c) BC = 32 cm; AC = 27 cm; b) AC = 9 cm; góc B bằng 470 d) BC = 5cm, góc C bằng 30° DẠNG 5: CHỨNG MINH ĐẲNG THỨC Bài 1. Chứng minh các đẳng thức sau: a) cos4 x – sin4 x = cos2 x – sin2 x b) sin4 x + cos2 x.sin2 x + sin2 x = 2sin2 x Bài 2. Chứng minh giá trị các biểu thức sau không phụ thuộc vào giá trị của góc nhọn α, β a) cos2 α.cos2 β + cos2 α.sin2 β + sin2 α b) 2(sinα – cosα)2 – (sinα + cosα)2 + 6sinα.cosα DẠNG 6: TÍNH GIÁ TRỊ CỦA BIỂU THỨC Bài 1. Tính giá trị của các biểu thức sau mà không dùng máy tính: A = sin2 150 + sin2 250 + sin2 350 + sin2 450 + sin2 550 + sin2 650 + sin2 750 Bài 2. Tính giá trị của các biểu thức sau (không dùng máy tính): Bài 3. DẠNG 7: BÀI TOÁN CÓ NỘI DUNG THỰC TẾ Bài 1. Tìm chiều cao của cây trong hình vẽ dưới đây: Bài 2. Một người dùng cách ngắm thước eke để đo chiều cao của một cái cây với cách đo được mô phỏng trong hình trên. Chiều cao tính từ chân đến mắt quan sát là 180cm và người này đứng thẳng cách gốc cây 240cm. Hãy tính chiều cao của cây. Bài 3. Hải đăng Trường Sa Lớn nằm trên đảo Trường Sa Lớn. Khi tia nắng mặt trời chiếu qua đỉnh của ngọn hải đăng hợp với mặt đất một góc 35 độ và bóng của ngọn hải đăng trên mặt đất dài 20m. Tính chiều cao ngọn hải đăng? Bài 4: Một hồ bơi hình chữ nhật, đường chéo dài 64 m. Góc tạo bởi đường chéo và chiều rộng là 680. Em hãy tính kích thước của hồ? ------ oOo ------ CHƯƠNG II: ĐƯỜNG TRÒN Bài 1. Cho điểm A nằm trên đường tròn (O; R). Từ A kẻ tiếp tuyến Ax và dây AB. Kẻ OM vuông góc với AB (M AB). Tia OM cắt Ax ở C. a) Chứng minh CO là đường trung trực của đoạn thẳng AB. b) Chứng minh CB là tiếp tuyến của đường tròn (O). c) Từ O kẻ đường thẳng vuông góc với OB, đường này cắt AC ở I. Đường thẳng vuông góc với OA tại O cắt BC ở E. Tứ giác OECI là hình gì ? Vì sao ? d) Trong trường hợp góc = 600, tính CM theo R. Bài 2. Cho ΔABC vuông tại A, có đường cao AH. Gọi K là trung điểm AH. Từ H, hạ vuông góc với AB và với AC tại D và E. Đường tròn tâm K bán kính AK cắt đường tròn tâm O đường kính BC tại I, AI cắt BC tại M. a) Chứng minh: 5 điểm A, I, D, H, E thuộc một đường tròn. b) Chứng minh: MK AO c) Chứng minh: 4 điểm M, D, K, E thẳng hàng. d) Chứng minh: MD. ME = MH2 Bài 3. Cho đường tròn (O; R) có AB là đường kính, dây cung AC = R. a) Tính các góc và cạnh BC của tam giác DABC theo R. b) Đường tròn tâm I đường kính OC cắt AC tại M, cắt BC tại N. Chứng minh: Tứ giác OMCN là hình chữ nhật. c) Tiếp tuyến tại C của (O) cắt ON tại E. Chứng minh BE là tiếp tuyến của đường tròn (O) d) Tính theo R diện tích tứ giác ECOB. Bài 4. Từ một điểm I ở ngòai đường tròn (O), kẻ một cát tuyến cắt (O) tại A và B. Các tiếp tuyến với đường tròn (O) tại A và B cắt nhau ở M. Hạ MH vuông góc với OI, MH cắt AB tại N, OM cắt AB tại K. a) Chứng minh: K là trung điểm của AB. b) Chứng minh: Năm điểm A, O, B, M, H cùng thuộc một đường tròn. c) Chứng minh: IA.IB = IK.IN d) MH cắt (O) tại C và D. Chứng tỏ IC, ID là các tiếp tuyến của (O). Bài 5. Cho ABC vuông tại A nội tiếp trong đường tròn (O; R) có đường kính BC và cạnh AB = R. Kẻ dây AD vuông góc với BC tại H. a) Tính độ dài các cạnh AC, AH và số đo các góc B, góc C. b) Chứng minh: AH.HD = HB.HC c) Gọi M là giao điểm của AC và BD. Qua M kẻ đường thẳng vuông góc với BC cắt BC ở I, cắt AB ở N. Chứng minh: C, D, N thẳng hàng. d) Chứng minh: AI là tiếp tuyến của đường tròn (O) và tính AI theo R. Bài 6. Cho (O; R) đường kính AB. Điểm C thuộc đường tròn (O) sao cho CA < CB. Vẽ dây CD vuông góc với AB tại H. Gọi E là điểm đối xứng với A qua H. a) CMR: tứ giác ACED là hình thoi. b) Đường tròn (I) đường kính EB cắt BC tại M. Chứng minh: D, E, M thẳng hàng. c) Chứng minh: HM là tiếp tuyến của đường tròn (I). d) Xác định vị trí điểm C trên đường tròn (O) sao cho. ------ oOo ------ "Đừng xấu hổ khi không biết, chỉ xấu hổ khi không học." (Khuyết danh) Thầy Cô chúc các em học sinh tích cực ôn tập và sẽ đạt kết quả tốt trong kiểm tra HK I nhé !
Tài liệu đính kèm:
 de_cuong_on_tap_hoc_ky_i_mon_toan_lop_9_nam_hoc_2020_2021_tr.docx
de_cuong_on_tap_hoc_ky_i_mon_toan_lop_9_nam_hoc_2020_2021_tr.docx



