Tổng hợp 100 bài tập môn Hình học Lớp 9

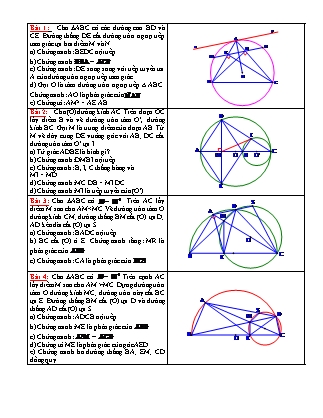
Bài 1: Cho DABC có các đường cao BD và CE. Đường thẳng DE cắt đường tròn ngoại tiếp tam giác tại hai điểm M và N.
a) Chứng minh: BEDC nội tiếp.
b) Chứng minh:.
c) Chứng minh: DE song song với tiếp tuyến tai A của đường tròn ngoại tiếp tam giác.
d) Gọi O là tâm đường tròn ngoại tiếp ∆ ABC. Chứng minh: AO là phân giác của
e) Chứng tỏ: AM2 = AE.AB.
Bài 2: Cho(O) đường kính AC. Trên đoạn OC lấy điểm B và vẽ đường tròn tâm O’, đường kính BC. Gọi M là trung điểm của đoạn AB. Từ M vẽ dây cung DE vuông góc với AB; DC cắt đường tròn tâm O’ tại I.
a) Tứ giác ADBE là hình gì?
b) Chứng minh: DMBI nội tiếp.
c) Chứng minh: B, I, C thẳng hàng và
MI = MD.
d) Chứng minh: MC.DB = MI.DC
d) Chứng minh: MI là tiếp tuyến của (O’)
Bài 3: Cho DABC có . Trên AC lấy điểm M sao cho AM<MC.Vẽ đường tròn tâm O đường kính CM; đường thẳng BM cắt (O) tại D; AD kéo dài cắt (O) tại S. 
a) Chứng minh: BADC nội tiếp.
b) BC cắt (O) ở E. Chứng minh rằng: MR là phân giác của .
c) Chứng minh: CA là phân giác của .
Bài 4: Cho DABC có .Trên cạnh AC lấy điểm M sao cho AM >MC. Dựng đường tròn tâm O đường kính MC; đường tròn này cắt BC tại E. Đường thẳng BM cắt (O) tại D và đường thẳng AD cắt (O) tại S.
a) Chứng minh: ADCB nội tiếp.
b) Chứng minh: ME là phân giác của .
c) Chứng minh: .
d) Chứng tỏ ME là phân giác của góc AED.
e) Chứng minh ba đường thẳng BA; EM; CD đồng quy.
 Bài 5: Cho DABC có 3 góc nhọn và AB < AC nội tiếp trong đường tròn tâm O. Kẻ đường cao AD và đường kính AA’. Gọi E, F theo thứ tự là chân đường vuông góc kẻ từ B và C xuống đường kính AA’.
a) Chứng minh: AEDB nội tiếp.
b) Chứng minh: DB.A’A = AD.A’C
c) Chứng minh: DE ^ AC.
d) Gọi M là trung điểm BC. Chứng minh:
 MD = ME = MF.
Bài 6: Cho DABC có ba góc nhọn nội tiếp trong đường tròn tâm O.Gọi M là một điểm bất kỳ trên cung nhỏ AC.Gọi E và F lần lượt là chân các đường vuông góc kẻ từ M đến BC và AC.P là trung điểm AB;Q là trung điểm FE.
a) Chứng minh: MFEC nội tiếp.
b) Chứng minh: BM.EF = BA.EM
c) Chứng minh: DAMP ∽ DFMQ.
d) Chứng minh: .
Bài 7: Cho (O) đường kính BC, điểm A nằm trên cung BC.Trên tia AC lấy điểm D sao cho AB = AD. Dựng hình vuông ABED; AE cắt (O) tại điểm thứ hai F; Tiếp tuyến tại B cắt đường thẳng DE tại G.
a) Chứng minhBGDC nội tiếp. Xác định tâm I của đường tròn này.
b) Chứng minhDBFC vuông cân và F là tâm đường tròn ngoại tiếp DBCD.
c) Chứng minh: GEFB nội tiếp.
c) Chứng tỏ:C, F, G thẳng hàng và G cũng nằm trên đường tròn ngoại tiếp DBCD. Có nhận xét gì về I và F
Bài 8: Cho DABC có 3 góc nhọn nội tiếp trong (O). Tiếp tuyến tại B và C của đường tròn cắt nhau tại D. Từ D kẻ đường thẳng song song với AB, đường này cắt đường tròn ở E và F, cắt AC ở I (E nằm trên cung nhỏ BC).
a) Chứng minhBDCO nội tiếp.
b) Chứng minh: DC2 = DE.DF.
c) Chứng minh:DOIC nội tiếp.
d) Chứng tỏ I là trung điểm FE.
Bài 9: Cho (O), dây cung AB. Từ điểm M bất kỳ trên cung AB(M ¹ A và M ¹ B), kẻ dây cung MN vuông góc với AB tại H. Gọi MQ là đường cao của DMAN.
a) Chứng minh4 điểm A, M, H, Q cùng nằm trên một đường tròn.
b) Chứng minh: NQ.NA =NH.NM
c) Chứng minh: MN là phân giác của.
d) Hạ đoạn thẳng MP vuông góc với BN; Xác định vị trí của M trên cung AB để 
MQ.AN + MP.BN có GTLN
Bài 10: Cho (O;R) và (I;r) tiếp xúc ngoài tại A (R > r). Dựng tiếp tuyến chung ngoài BC (B nằm trên đường tròn tâm O và C nằm trên đư ờng tròn tâm (I). Tiếp tuyến BC cắt tiếp tuyến tại A của hai đường tròn ở E.	
a) Chứng minh tam giác ABC vuông ở A.
b) O E cắt AB ở N ; IE cắt AC tại F. Chứng minh N, E, F, A cùng nằm trên một đường tròn 
c) Chứng tỏ : BC2 = 4Rr
d) Tính diện tích tứ giác BCIO theo R, r
Bài 11: Trên hai cạnh góc vuông xOy lấy hai điểm A và B sao cho OA = OB. Một đường thẳng qua A cắt OB tại M (M nằm trên đoạn OB). Từ B hạ đường vuông góc với AM tại H, cắt AO kéo dài tại I.
a) Chứng minhOMHI nội tiếp.
b) Tính góc OMI.
c) Từ O vẽ đường vuông góc với BI tại K. Chứng minh: OK = KH
d) Tìm tập hợp các điểm K khi M thay đổi trên OB.
Bài 12: Cho (O) đường kính AB và dây CD vuông góc với AB tại F. Trên cung BC lấy điểm M.Nối A với M cắt CD tại E.
a) Chứng minh: AM là phân giác của góc CMD.
b) Chứng minh: EFBM nội tiếp.
c) Chứng tỏ: AC2 = AE.AM
d) Gọi giao điểm CB với AM là N; MD với AB là I. Chứng minh: NI //CD
e) Chứng minh N là tâm đường tròn nội tiếp DCIM
Bài 13: Cho (O) và điểm A nằm ngoài đường tròn. Vẽ các tiếp tuyến AB; AC và cát tuyến ADE. Gọi H là trung điểm DE.
a) Chứng minh: A, B, H, O, C cùng nằm trên 1 đường tròn.
b) Chứng minh: HA là phân giác của .
c) Gọi I là giao điểm của BC và DE. Chứng minh: AB2 = AI.AH.
d) BH cắt (O) ở K.Chứng minh: AE // CK.
Bài 14: Cho (O) đường kính AB = 2R, xy là tiếp tuyến với (O) tại B. CD là 1 đường kính bất kỳ. Gọi giao điểm của AC, AD với xy theo thứ tự là M, N.
a) Cmr: MCDN nội tiếp.
b) Chứng tỏ: AC.AM = AD.AN
c) Gọi I là tâm đường tròn ngoại tiếp tứ giác MCDN và H là trung điểm MN. Cmr: AOIH là hình bình hành.
d) Khi đường kính CD quay xung quanh điểm O thì I di động trên đường nào?
Bài 15: Cho tam giác ABC nội tiếp trong đường tròn tâm O. Gọi D là 1 điểm trên cung nhỏ BC.Kẻ DE;DF;DG lần lượt vuông góc với các cạnh AB, BC, AC. Gọi H là hình chiếu của D lên tiếp tuyến Ax của (O).
a) Chứng minh: AHED nội tiếp
b) Gọi giao điểm của AE với HD và HB với (O) là P và Q, ED cắt (O) tại M. 
Chứng minh: HA.DP = PA.DE
c) Chứng minh: QM = AB
d) Chứng minh: DE.DG = DF.DH
e) Chứng minh: E, F, G thẳng hàng (đường thẳng Sim sơn)
Bài 16: Cho tam giác ABC có , AB < AC. Gọi I là trung điểm BC;qua I kẻ IK ^ BC (K nằm trên BC). Trên tia đối của tia AC lấy điểm M sao cho MA = AK.
a) Chứng minh: ABIK nội tiếp được trong đường tròn tâm I.
b) Chứng minh: 
c) Chứng tỏ BC2 = 2AC.KC
d) AI kéo dài cắt đường thẳng BM tại N. Chứng minh AC = BN
Bài 17: Cho (O) đường kính AB cố định,điểm C di động trên nửa đường tròn.Tia phân giác của ACB cắt (O) tai M.Gọi H;K là hình chiếu của M lên AC và BC.
a) Chứng minh:MOBK nội tiếp.
b) Tứ giác CKMH là hình vuông.
c) Chứng minhH;O;K thẳng hàng.
d) Gọi giao điểm HKvà CM là I.Khi C di động trên nửa đường tròn thì I chạy trên đường nào?
Bài 18: Cho hình chữ nhật ABCD có AB = 2a, 
BC = a. Kẻ tia phân giác của , từ A hạ AH vuông góc với đường phân giác nói trên.
a) Chứng minh: AHDC nội tiếp trong ( O) mà ta phải định rõ tâm và bán kính theo a.
b) HB cắt AD tại I và cắt AC tại M; HC cắt DB tại N. Chứng tỏ HB = HC. Và AB.AC = BH.BI
c) Chứng tỏ MN song song với tiếp tuyến tại H của (O)
d) Từ D kẻ đường thẳng song song với BH; đường này cắt HC ở K và cắt (O) ở J. Chứng minh HOKD nội tiếp.
Bài 19: Cho nửa đường tròn (O) đường kính AB, bán kính OC ^ AB. Gọi M là 1 điểm trên cung BC. Kẻ đường cao CH của DACM.
a) Chứng minh AOHC nội tiếp.
b) Chứng tỏ DCHM vuông cân và OH là phân giác của .
c) Gọi giao điểm của OH với BC là I. MI cắt (O) tại D. Cmr: CDBM là hình thang cân.
d) BM cắt OH tại N. 
Chứng minh: DBNI ∽ DAMC, từ đó suy ra: BN.MC = IN.MA.
Bài 20: Cho Dđều ABC nội tiếp trong (O;R). Trên AB và AC lấy hai điểm M; N sao cho 
BM = AN.
a) Chứng tỏ DOMN cân.
b) Chứng minh: OMAN nội tiếp.
c) BO kéo dài cắt AC tại D và cắt (O) ở E. Chứng minh: BC2 + DC2 = 3R2.
d) Đường thẳng CE và AB cắt nhau ở F. Tiếp tuyến tại A của (O) cắt FC tại I; AO kéo dài cắt BC tại J. Chứng minh: BI đi qua trung điểm của AJ.
Bài 21: Cho DABC ()nội tiếp trong đường tròn tâm (O). Gọi M là trung điểm cạnh AC. Đường tròn tâm I đường kính MC cắt cạnh BC ở N và cắt (O) tại D.
a) Chứng minh tứ giác ABNM nội tiếp và CN.AB = AC.MN.
b) Chứng tỏ B, M, D thẳng hàng và OM là tiếp tuyến của (I).
c) Tia IO cắt đường thẳng AB tại E. Chứng minh BMOE là hình bình hành.
d) Chứng minh NM là phân giác của .
Bài 22: Cho hình vuông ABCD có cạnh bằng a. Gọi I là điểm bất kỳ trên đường chéo AC. Qua I kẻ các đường thẳng song song với AB; BC, các đường này cắt AB; BC; CD; DA lần lượt ở P; Q; N; M
a) Chứng minh INCQ là hình vuông.
b) Chứng tỏ NQ // DB.
c) BI kéo dài cắt MN tại E; MP cắt AC tại F. Chứng minh MFIN nội tiếp được trong đường tròn. Xác định tâm.
d) Chứng tỏ MPQN nội tiếp. Tính diện tích của nó theo a.
e) Chứng minh: MFIE nội tiếp.
Bài 23: Cho hình vuông ABCD, N là trung điểm DC; BN cắt AC tại F. Vẽ đường tròn tâm O đường kính BN. (O) cắt AC tại E. BE kéo dài cắt AD ở M; MN cắt (O) tại I.
a) Chứng minh MDNE nội tiếp.
b) Chứng tỏ DBEN vuông cân.
c) Chứng minh MF đi qua trực tâm H của DBMN
d) Chứng minh BI = BC và DIE F vuông.
e) NE cắt AB tại Q. Chứng minh MQBN là hình thang cân
Bài 24: Cho DABC có 3 góc nhọn(AB < AC). Vẽ đường cao AH. Từ H kẻ HK; HM lần lượt vuông góc với AB; AC. Gọi J là giao điểm của AH và MK.
a) Chứng minh AMHK nội tiếp.
b) Chứng minh JA.JH = JK.JM
c) Từ C kẻ tia Cx vuông góc với AC và Cx cắt AH kéo dài ở D. Vẽ HI; HN lần lượt vuông góc với DB và DC. Cmr : 
d) Chứng minh M; N; I; K cùng nằm trên một đường tròn.
Bài 25: Cho DABC (), đường cao AH. Đường tròn tâm H, bán kính HA cắt đường thẳng AB tại D và cắt AC tại E; Trung tuyến AM của DABC cắt DE tại I.
a) Chứng minh D; H; E thẳng hàng.
b) Chứng minh BDCE nội tiếp. Xác định tâm O của đường tròn này.
c) Chứng minh AM ^ DE.
d) Chứng minh AHOM là hình bình hành.
Bài 26: Cho DABC có 3 góc nhọn, đường cao AH. Gọi K là điểm dối xứng của H qua AB; I là điểm đối xứng của H qua AC. E; F là giao điểm của KI với AB và AC.
a) Chứng minh: AICH nội tiếp.
b) Chứng minh: AI = AK
c) Chứng minh: Các điểm: A, E, H, C, I cùng nằm trên một đường tròn.
d) Chứng minh: CE; BF là các đường cao của DABC
e) Chứng tỏ giao điểm 3 đường phân giác của DHFE chính là trực tâm của DABC.
Bài 27: Cho DABC (AB =AC) nội tiếp trong (O). Gọi M là một điểm bất kỳ trên cung nhỏ AC. Trên tia BM lấy MK = MC và trên tia BA lấy 
AD = AC.
a) Chứng minh: 
b) Chứng minh: BCKD nội tiếp. Xác định tâm của đường tròn này.
c) Gọi giao điểm của DC với (O) là I. Chứng minh: B; O; I thẳng hàng.
d) Chứng minh: DI = BI.
Bài 28: Cho tứ giác ABCD nội tiếp trong (O). Gọi I là điểm chính giữa cung AB (Cung AB không chứa điểm C, D). IC và ID cắt AB ở M; N.
a) Chứng minh: D, M, N, C cùng nằm trên một đường tròn.
b) Chứng minh: NA.NB=NI.NC
c) DI kéo dài cắt đường thẳng BC ở F; đường thẳng IC cắt đường thẳng AD ở E. Chứng minh: EF //AB
d) Chứng minh:IA2 = IM.ID.
Bài 29: Cho hình vuông ABCD, trên cạnh BC lấy điểm E. Dựng tia Ax vuông góc với AE, Ax cắt cạnh CD kéo dài tại F. Kẻ trung tuyến AI của DAEF, AI kéo dài cắt CD tại K. Qua E dựng đường thẳng song song với AB, cắt AI tại G.
a) Chứng minh: AECF nội tiếp.
b) Chứng minh: AF2 = KF.CF
c) Chứng minh: EGFK là hình thoi.
d) Cmr: khi E di động trên BC thì EK = BE + DK và chu vi DCKE có giá trị không đổi.
e) Gọi giao điểm của EF với AD là J. Chứng minh: GJ ^ JK.
Bài 30: Cho DABC. Gọi H là trực tâm của tam giác. Dựng hình bình hành BHCD. Gọi I là giao điểm của HD và BC.
a) Chứng minh: ABDC nội tiếp trong đường tròn tâm O; nêu cáh dựng tâm O.
b) So sánh và.
c) CH cắt OD tại E. Chứng minh: AB.AE = AH.AC
d) Gọi giao điểm của AI và OH là G. Chứng minh: G là trọng tâm của DABC.
Bài 31: Cho (O) và cung AB = 90o. C là điểm tuỳ ý trên cung lớn AB. Các đường cao AI, BK, CJ của DABC cắt nhau ở H. BK cắt (O) ở N; AH cắt (O) tại M. BM và AN gặp nhau ở D.
a) Chứng minh: B, K, C, J cùng nằm trên một đường tròn.
b) Chứng minh: BI.KC = HI.KB
c) Chứng minh:MN là đường kính của (O)
d) Chứng minh: ACBD là hình bình hành.
e) Chứng minh: OC // DH.
Bài 32: Cho hình vuông ABCD. Gọi N là một điểm bất kỳ trên CD sao cho CN < ND; Vẽ đường tròn tâm O đường kính BN. (O) cắt AC tại F; BF cắt AD tại M; BN cắt AC tại E.
a) Chứng minh:DBFN vuông cân.
b) Chứng minh: MEBA nội tiếp 
c) Gọi giao điểm của ME và NF là Q. MN cắt (O) ở P. Chứng minh: B, Q, P thẳng hàng.
d) Chứng tỏ ME // PC và BP = BC.
e) Chứng minh : DFPE là tam giác vuông
Bài 33: Trên đường tròn tâm O lần lượt lấy bốn điểm A, B, C, D sao cho AB = DB; AB và CD cắt nhau ở E. BC cắt tiếp tuyến tại A của đường tròn(O) ở Q; DB cắt AC tại K.
a) Chứng minh: CB là phân giác của.
b) Chứng minh: AQEC nội tiếp.
c) Chứng minh: KA.KC = KB.KD
d) Chứng minh: QE//AD.
Bài 34: Cho (O) và tiếp tuyến Ax. Trên Ax lấy hai điểm B và C sao cho AB = BC. Kẻ cát tuyến BEF với đường tròn. CE và CF cắt (O) lần lượt ở M và N. Dựng hình bình hành AECD.
a) Chứng minh: D nằm trên đường thẳng BF.
b) Chứng minh: ADCF nội tiếp.
c) Chứng minh: CF.CN = CE.CM
d) Chứng minh: MN//AC.
e) Gọi giao điểm của AF với MN là I. Cmr: DF đi qua trung điểm của NI.
Bài 35: Cho (O;R) và đường kính AB; CD vuông góc với nhau. Gọi M là một điểm trên cung nhỏ CB.
a) Chứng minh: ACBD là hình vuông.
b) AM cắt CD, CB lần lượt ở P và I. Gọi J là giao điểm của DM và AB. Chứng minh : 
IB.IC = IA.IM
c) Chứng tỏ IJ//PD và IJ là phân giác của.
d) Tính diện tích DAID theo R.
Bài 37: Cho DABC (). Kẻ AH ^ BC. Gọi O và O’ là tâm đường tròn nội tiếp DAHB và DAHC. Đường thẳng OO’ cắt cạnh AB, AC tại M, N.
a) Chứng minh: D OHO’ là tam giác vuông.
b) Chứng minh: HB.HO’ = HA.HO
c) Chứng minh: DHOO’ ∽ DHBA.
d) Chứng minh: Các tứ giác BMHO; HO’NC nội tiếp.
e) Chứng minh: DAMN vuông cân.
Bài 37: Cho nửa đường tròn O, đường kính AB = 2R, gọi I là trung điểm AO. Qua I dựng đường thẳng vuông góc với AB, đường này cắt nửa đường tròn ở K. Trên IK lấy điểm C, AC cắt (O) tại M; MB cắt đường thẳng IK tại D. Gọi giao điểm của IK với tiếp tuyến tại M là N.
a) Chứng minh:AIMD nội tiếp.
b) Chứng minh: CM.CA = CI.CD.
c) Chứng minh: ND = NC.
d) CB cắt AD tại E. Chứng minh: E nằm trên đường tròn (O) và C là tâm đường tròn nội tiếp DEIM.
e) Giả sử C là trung điểm IK.Tính CD theo R.
Bài 38: Cho DABC. Gọi P là một điểm nằm trong tam giác sao cho . Gọi H và K lần lượt là chân các đường vuông góc hạ từ P xuống AB, AC.
a) Chứng minh: AHPK nội tiếp.
b) Chứng minh: HB.KP = HP.KC.
c) Gọi D, E, F lần lượt là trung điểm của PB, PC, BC. Cmr: HD = EF; DF = EK
d) Chứng minh: Đường trung trực của HK đi qua F.
Bài 39: Cho hình bình hành ABCD(). Từ C kẻ CE, CF, CG lần lượt vuông góc với AD, DB, AB.
a) Chứng minh: DEFC nội tiếp.
b) Chứng minh: CF2 = EF.GF.
c) Gọi O là giao điểm AC và DB. Kẻ OI ^ CD. Cmr: OI đi qua trung điểm của AG.
d) Chứng tỏ EOFG nội tiếp.
Bài 40: Cho hai đường tròn (O) và (O’) cắt nhau ở A và B. Các đường thẳng AO cắt (O), (O’) lần lượt ở C và E; đường thẳng AO’ cắt (O) và (O’) lần lượt ở D và F.
a) Chứng minh: C, B, F thẳng hàng.
b) Chứng minh: CDEF nội tiếp.
c) Chứng tỏ DA.FE = DC.EA
d) Chứng minhA là tâm đường tròn nội tiếp DBDE.
e) Tìm điều kiện để DE là tiếp tuyến chung của hai đường tròn (O); (O’)
Bài 41: Cho (O;R). Một cát tuyến xy cắt (O) ở E và F. Trên xy lấy điểm A nằm ngoài đoạn EF, vẽ 2 tiếp tuyến AB và AC với (O). Gọi H là trung điểm EF.
a) Chứng tỏ 5 điểm: A, B, C, O, H cùng nằm trên một đường tròn.
b) Đường thẳng BC cắt OA ở I và cắt đường thẳng OH ở K. Chứng minh: OI.OA = OH.OK = R2.
c) Khi A di động trên xy thì I di động trên đường nào?
d) Chứng minh: KE và KF là hai tiếp tyuến của (O)
Bài 42: Cho DABC (AB < AC) có hai đường phân giác CM, BN cắt nhau ở D. Qua A kẻ AE và AF lần lượt vuông góc với BN và CM. Các đường thẳng AE và AF cắt BC ở I; K.
a) Chứng minh: AFDE nội tiếp.
b) Chứng minh: AB.NC = BN.AB
c) Chứng minh: FE // BC
d) Chứng tỏ ADIC nội tiếp.	
{Chú ý bài toán vẫn đúng khi AB > AC}
Bài 43: Cho DABC (); AB = 15; 
AC = 20 (cùng đơn vị đo độ dài). Dựng đường tròn tâm O đường kính AB và (O’) đường kính AC. Hai đường tròn (O) và (O’) cắt nhau tại điểm thứ hai D.
a) Chứng tỏ D nằm trên BC.
b) Gọi M là điểm chính giữa cung nhỏ DC. AM cắt DC ở E và cắt (O) ở N. Chứng minh:
 DE.AC = AE.MC
c) Chứng minh: AN = NE và O; N; O’ thẳng hàng.
d) Gọi I là trung điểm MN. Chứng minh: .
e) Tính diện tích ∆ AMC.
Bài 44: Trên (O;R), ta lần lượt đặt theo một chiều, kể từ điểm A một cung AB bằng 600, rồi cung BC bằng 900 và cung CD bằng 1200.
a) Chứng minh: ABCD là hình thang cân.
b) Chứng tỏ AC ^ DB.
c) Tính các cạnh và các đường chéo của ABCD
d) Gọi M; N là trung điểm các cạnh DC và AB. Trên DA kéo dài về phía A lấy điểm P; PN cắt DB tại Q. Chứng minh: MN là phân giác của .
Bài45: Cho D đều ABC có cạnh bằng a. Gọi D là giao điểm hai đường phân giác góc A và góc B của ∆ABC. Từ D dựng tia Dx vuông góc với DB. Trên Dx lấy điểm E sao cho ED = DB (D và E nằm hai phía của đường thẳng AB). Từ E kẻ EF ^ BC. Gọi O là trung điểm EB.
a) Chứng minh: AEBC và EDFB nội tiếp, xác định tâm và bán kính của các đường tròn ngoại tiếp các tứ giác trên theo a.
b) Kéo dài FE về phía F,cắt (D) tại M. EC cắt (O) ở N. Chứng minh: EBMC là thang cân. Tính diện tích.
c) Chứng minh: CE là phân giác của .
d) Chứng minh: FD là đường trung trực của MB
e) Chứng tỏ A; D; N thẳng hàng.
f) Tính diện tích phần mặt trăng được tạo bởi cung nhỏ EB của hai đường tròn.
Bài 46: Cho nửa đường tròn (O) đường kính BC. Gọi A là một điểm bất kỳ trên nửa đường tròn; BA kéo dài cắt tiếp tuyến Cy ở F. Gọi D là điểm chính giữa cung AC; DB kéo dài cắt tiếp tuyến Cy tại E.
a) Chứng minh: BD là phân giác của và OD // AB.
b) Chứng minh: ADEF nội tiếp.
c) Gọi I là giao điểm BD và AC. Chứng tỏ:
 CI = CE và IA.IC = ID.IB.
d) Chứng minh: 
Bài47: Cho nửa đtròn (O); đường kính AD. Trên nửa đường tròn lấy hai điểm B và C sao cho cung AB < AC; AC cắt BD ở E. Kẻ 
EF ^ AD tại F.
a) Chứng minh: ABEF nội tiếp.
b) Chứng tỏ: DE.DB = DF.DA.
c) Chứng minh: E là tâm đường tròn nội tiếp DFBC. 
d) Gọi I là giao điểm BD với CF. Chứng minh: BI2 = BF.BC – IF.IC
Bài 48: Cho (O) đường kính AB; P là một điểm di động trên cung AB sao cho PA < PB. Dựng hình vuông APQR vào phía trong đường tròn. Tia PR cắt (O) tại C.
a) Chứng minh: DACB vuông cân.
b) Vẽ phân giác AI của (I nằm trên(O); AI cắt PC tại J. Chứng minh4 điểm J; A; Q; B cùng nằm trên một đường tròn.
c) Chứng tỏ: CI.QJ = CJ.QP.
Bài 49: Cho nửa (O) đường kính AB = 2R. Trên nửa đường tròn lấy điểm M sao cho . Tiếp tuyến với nửa đường tròn tại M cắt tiếp tuyến Ax và By lần lượt ở D và C.
a) Chứng tỏ ADMO nội tiếp.
b) Chứng tỏ AD.BC = R2.
c) Đường thẳng DC cắt đường thẳng AB tại N; MO cắt Ax ở F; MB cắt Ax ở E. Chứng minh: AMFN là hình thang cân.
d) Xác định vị trí của M trên nửa đường tròn để DE = EF
Bài 50: Cho hình vuông ABCD, E là một điểm thuộc cạnh BC. Qua B kẻ đường thẳng vuông góc với DE, đường này cắt các đường thẳng DE và DC theo thứ tự ở H và K.
a) Chứng minh: BHCD nội tiếp. 
b) Tính góc CHK.
c) Chứng minh: KC.KD = KH.KB.
d) Khi E di động trên BC thì H di động trên đường nào?