Đề kiểm tra giữa học kỳ I môn Toán Lớp 8 - Năm học 2020-2021 - Trường THCS Võ Xán

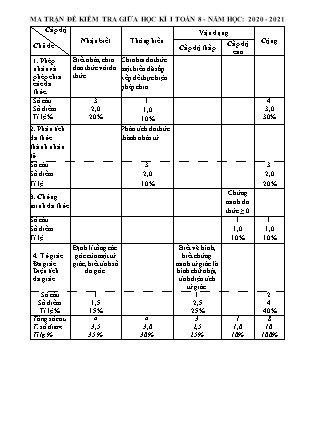
MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KÌ I TOÁN 8 - NĂM HỌC: 2020 - 2021
 Cấp độ
Chủ đề 
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
1. Phép nhân và phép chia các đa thức.
Biết nhân, chia đơn thức với đa thức.
Chia hai đa thức một biến đã sắp xếp để thực hiện phép chia 
Số câu
Số điểm
Tỉ lệ %
3
2,0
20%
1
1,0
10%
4
3,0
30%
2. Phân tích đa thức thành nhân tử
Phân tích đa thức thành nhân tử
Số câu
Số điểm
Tỉ lệ
3
2,0
10%
3
2,0
20%
3. Chứng minh đa thức
Chứng minh đa thức ≥ 0
Số câu
Số điểm
Tỉ lệ
1
1,0
10%
1
1,0
10%
4. Tứ giác. Đa giác. Diện tích đa giác.
Định lí tổng các góc của một tứ giác, biết tính số đo góc.
Biết vẽ hình, biết chứng minh tứ giác là hình chữ nhật, tính diện tích tứ giác. 
Số câu
Số điểm
Tỉ lệ %
1
1,5
15%
1
2,5
25%
2
4
40%
Tổng số câu 
T. số điểm
Tỉ lệ %
4
3,5
35 %
4
3,0
30 %
3
2,5
25 %
1
1,0
10%
 8
10 
100%
PHÒNG GD&ĐT HUYỆN TÂY SƠN
TRƯỜNG THCS VÕ XÁN
ĐỀ KIỂM TRA GIỮA HỌC KỲ I – TOÁN 8
NĂM HỌC: 2020 – 2021
Thời gian: 90 phút
(Không kể thời gian phát đề)
Điểm
Lời nhận xét của giáo viên
ĐỀ BÀI:
Bài 1. (1,5 điểm)
 a) Phát biểu định lí tổng bốn góc của một tứ giác. 
b) Cho tứ giác MNPQ có: . Tính số đo góc Q?
Bài 2 (3,0 điểm): Thực hiện các yêu cầu sau:
1. Làm tính nhân: 
a) 7x2.(2x3 + 3x5) 	b) (x3 + 5y2).( x2 – 3x2 + 7y3)
2. Làm tính chia:
	a) 48x7y2z : 6x2y3	b) (2x4 – 3x3 + 3x2 – 3x + 1) : (x2 + 1)	
Bài 3. (2,0 điểm): Phân tích các đa thức sau thành nhân tử:
	a) 3x2 + 6xy 	b) x2 – 2xy + 3x – 6y	 c) x2 - 8x + 7
Bài 4. (2,5 điểm): 
	Cho tam giác ABC vuông tại A, M là trung điểm của BC. Kẻ MD // AB, ME // AC (D AC, E AB). 
Chứng minh tứ giác ADME là hình chữ nhật.
Cho AM = 10cm, AD = 6cm. Tính diện tích tứ giác ADME?
Bài 5. (1,0 điểm): Chứng minh rằng: với mọi .
----Hết----
BÀI LÀM
ĐÁP ÁN VÀ THANG ĐIỂM
Câu hỏi
Đáp án
Điểm
Bài 1: 
(1,5 điểm)
a) Định lí: Tổng các góc của một tứ giác bằng 360
0,75đ
b) Theo định lí tổng các góc của một tứ giác, ta có:
0,25đ
0,25đ
0,25đ
Bài 2:
(3,0 điểm)
a) 7x2.(2x3 + 3x5) = 14x5 + 21x7
b) (x3 + 5y2).( x2 – 3x2 + 7y3)
= x5 – 3x5 +7x3y3 +5x2y2 +15x2y2 +35y5
= -2x5 + 35y5 + 20 x2y2
0,5đ
1,0đ
a) 48x7y3z : 6x2y3 = 8x5z
b) (2x4 – 3x3 + 3x2 – 3x + 1) : (x2 + 1) = 2x2 – 3x + 1
0,5đ
1,0đ
Bài 3:
(2,0 điểm)
a/ 3x2 + 6xy = 3x(x + 2y)
b/ x2 – 2xy + 3x – 6y = (x2 – 2xy)+ (3x – 6y)
 = x(x – 2y) + 3(x – 2y) 
 = (x – 2y)(x + 3)
c/ x2 - 8x + 7 = (x2 - 7x )-(x - 7) = x(x-7) - (x - 7) = ( x- 7)(x -1)
0,5đ
1,0đ
0,5đ
Bài 4:
(2,5 điểm)
 Vẽ hình đúng
0,5đ
a) Xét tứ giác ADME có:
MD // AB, ME // AC (gt)
=> ADME là hình bình hành (dấu hiệu)
Có (gt) 
=> ADME là hình chữ nhật (dấu hiệu)
0,25đ
0,25đ
0,25đ
0,25đ
b) Vì ADME là hình chữ nhật nên 
Áp dụng định lý Py-ta-go cho tam giác AMD vuông tại D, ta có: 
hay 
= 64 MD = 8 (cm)
Vậy diện tích của hình chữ nhật ADME là: 
(cm2).
0,25đ
0,25đ
0,25đ
0,25đ
Bài 5:
(1,0 điểm)
Ta có: 
Ta luôn có: với mọi x với mọi x 
0,5đ
0,5đ
HS làm cách khác vẫn đạt điểm tối đa!
Hết!