Đề kiểm tra giữa học kỳ I môn Toán Lớp 9 - Năm học 2020-2021 (có đáp án)
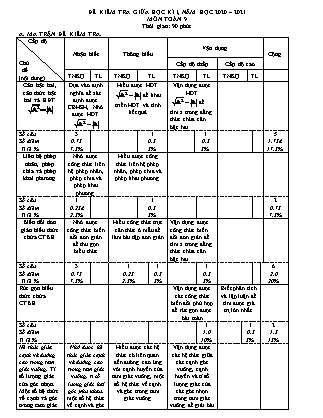
Câu 1. Điều kiện xác định của : A. B. C. D.
Câu 2. Khử mẫu của biểu thức lấy căn: ta được biểu thức là:
A. B. C. D.
Câu 3. Căn bậc hai số học của 5 là : A. 25 B. 5 C. D. 5
Câu 4. Đẳng thức nào sau đây là đúng:
A. B.
C. D.
Câu 5. bằng: A. 5 B. C. - D. –
Câu 6. Trục căn thức ở mẫu của biểu thức (với 0 và a 1), ta được:
A. B. C. D.
Câu 7: bằng A. 25 B. 5 C. 625 D. 12,5
Câu 8: Giá trị biểu thức bằng: A. 1 B. 22 C. 10 D. 42
Câu 9: Hệ thức nào sau đây là đúng:
A. sin 600 = cos300 B. tan 400 = cot400
C. cot2 800 + tan 2100 = 1 D. sin 500 = cos500
Câu 10: Cho tam giác ABC vuông tại A, đường cao AH. Hệ thức nào sao đây sai?
A. AB.BC = AC.AH ; B. BC.BH = AB2 ;
C. AC2 = HC.BC D. AH2 = HB.HC
Câu 11: Tam giác ABC vuông tại A và góc B = 300 ; BC = 8, khi đó AC =?
A. 8.cos300 B. 8.sin300 C. 8.tan300 D. 8 cot 300
Câu 12: Rút gọn biểu thức với a < 3="" ta="">
A. a2(3 – a ) B. a2(a + 3 ) C. a2(a - 3 ) D. -a2(a + 3 )
ĐỀ KIỂM TRA GIỮA HỌC KÌ I, NĂM HỌC 2020 – 2021 MÔN TOÁN 9 Thời gian: 90 phút A. MA TRẬN ĐỀ KIỂM TRA. Cấp độ Chủ đề (nội dung) Nhận biết Thông hiểu Vận dụng Cộng Cấp độ thấp Cấp độ cao TNKQ TL TNKQ TL TNKQ TL TNKQ TL Căn bậc hai, căn thức bậc hai và HĐT Dựa vào định nghĩa để xác định được CBHSH, Nhớ được HĐT Hiểu được HĐT để khai triển HĐT và tính kết quả Vận dụng được HĐT để tìm x trong đẳng thức chứa căn bậc hai. Số câu Số điểm Tỉ lệ % 3 0.75 7,5% 1 0,5 5% 1 0,5 5% 5 1,75đ 17.5% Liên hệ phép nhân, phép chia và phép khai phương Nhớ được công thức liên hệ phép nhân, phép chia và phép khai phương Hiểu được công thức liên hệ phép nhân, phép chia và phép khai phương Số câu Số điểm Tỉ lệ % 1 0.25đ 2,5% 1 0,5 5% 2 0,75 7.5% Biến đổi đơn giản biểu thức chứa CTBH Nhớ được công thức biến đổi đơn giản để thu gọn biểu thức Hiểu công thức trục căn thức ở mẫu để làm bài tập đơn giản Vận dụng được công thức biến đổi đơn giản để tìm x trong đẳng thức chứa căn bậc hai. Số câu Số điểm Tỉ lệ % 3 0.75 7,5% 1 0,25 2,5% 1 0,5 5% 1 0,5 5% 6 2,0 20% Rút gọn biểu thức chứa CTBH Vận dụng được các công thức biến đổi phù hợp để rút gọn được bài toán Biết phân tích và lập luận để tìm được giá trị lớn nhất. Số câu Số điểm Tỉ lệ % 1 1,0 10% 1 0,5 5% 2 1,5 15% Hệ thức giữa cạnh và đường cao trong tam giác vuông. Tỉ số lượng giác của góc nhọn. Một số hệ thức về cạnh và góc trong tam giác vuông Nhớ được hệ thức giữa cạnh và đường cao trong tam giác vuông, tỉ số lượng giác hai góc phụ nhau, một số hệ thức về cạnh và góc trong tam giác vuông Hiểu được các hệ thức có liên quan đến đường cao ứng với cạnh huyền của tam giác vuông, một số hệ thức về cạnh và góc trong tam giác vuông Vận dụng được các hệ thức giữa các cạnh góc vuông, cạnh huyền và tỉ số lượng giác của các góc nhọn trong tam giác vuông để giải bài tập, chứng minh hai tam giác đồng dạng . 3 0.75 7,5% 1 0,25 2,5% 1 1 10% 2 2,0 20% 7 4 40% Tổng số câu Tổng sốđiểm Tỉ lệ % 10 2,5 25% 2 0.5 5% 4 2,5 25% 5 4,0 40% 1 0,5 5% 22 10 =100% Câu 1. Điều kiện xác định của : A. B. C. D. Câu 2. Khử mẫu của biểu thức lấy căn: ta được biểu thức là: A. B. C. D. Câu 3. Căn bậc hai số học của 5 là : A. 25 B. 5 C. D. 5 Câu 4. Đẳng thức nào sau đây là đúng: A. B. C. D. Câu 5. bằng: A. 5 B. C. - D. – Câu 6. Trục căn thức ở mẫu của biểu thức (với 0 và a1), ta được: A. B. C. D. Câu 7: bằng A. 25 B. 5 C. 625 D. 12,5 Câu 8: Giá trị biểu thức bằng: A. 1 B. 22 C. 10 D. 42 Câu 9: Hệ thức nào sau đây là đúng: A. sin 600 = cos300 B. tan 400 = cot400 C. cot2 800 + tan 2100 = 1 D. sin 500 = cos500 Câu 10: Cho tam giác ABC vuông tại A, đường cao AH. Hệ thức nào sao đây sai? A. AB.BC = AC.AH ; B. BC.BH = AB2 ; C. AC2 = HC.BC D. AH2 = HB.HC Câu 11: Tam giác ABC vuông tại A và góc B = 300 ; BC = 8, khi đó AC =? A. 8.cos300 B. 8.sin300 C. 8.tan300 D. 8 cot 300 Câu 12: Rút gọn biểu thức với a < 3 ta được: A. a2(3 – a ) B. a2(a + 3 ) C. a2(a - 3 ) D. -a2(a + 3 ) II. TỰ LUẬN (7điểm) Câu 1 (1,5 điểm). Rút gọn các biểu thức sau: a. A = b)B = c) C = Câu 2 (1,0 điểm). Tìm x biết. a) b) Câu 3 (1,0 điểm). Cho biểu thức ; với a) Rút gọn biểu thức P . b) Tìm điều kiện của x để P > 0 Câu 4(4,0 điểm) Cho tam giác ABC vuông tại A. a) Giả sử khi AB = 9; AC = 12. Tính cạnh BC và các góc còn lại của tam giác ABC ( Làm tròn đến độ) b) Gọi H là hình chiếu của A trên BC; E, F lần lượt là hình chiếu của H trên AB, AC. Chứng minh rằng: AH = EF và AE.AB = AF.AC c) Gọi K là trung điểm của BC, biết AK cắt ÈF tại I. Chứng tỏ rằng AK vuông góc với EF. Câu 5 (1,0 điểm) Cho các số thực x, y thỏa mãn: . Tìm GTNN của biểu thức A= C. ĐÁP ÁN - BIỂU ĐIỂM: I TRẮC NGHIỆM Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án D C C D A B B D A A B A CÂU PHẦN NỘI DUNG ĐIỂM 1 (1,5 điểm) a = = . Vậy A = 0.25 0.25 b B = = 12 – 10 = 2 0.25 0.25 c = == 4 – 7 = -3 0.25 0.25 2 (1,0 điểm) a a) 6 - 3 = 2+ = 1 x + 3 = 1 x = -2 (T/m ĐK) Vậy PT có nghiệm là x = -2 0,25 0,25 b b) - ĐKXĐ: với mọi x R Ta có: = 2017 =2013 (t/m) Vậy phương trình có tập nghiệm là S = 0,25 0,25 3 (1,0 điểm) a)với . Ta có: = = . Vậy P = với b) Để P > 0 < 0 vì -3< 0 x < 9 Vậy 0 0 0,25 0,25 0,25 0,25 4 (3,0 điểm) a - Vẽ hình đúng, ghi GT, KL ( vẽ hình sai, không chấm) a) - AD Pytago tính được BC = 15 ( đvđd) - Tính được ; Vậy BC = 15 ( đvđd) ; ; 0,25 0,25 0,25 0,25 b b) Xét AHB vuông tại H có HE AB. Áp dụng hệ thức lượng trong tam giác vuông có: ta có: AH2 = AE.AB - Tương tự, ta có AH2 = AF.AC AE.AB = AF.AC - Chứng minh được tứ giác AEHF là hình chữ nhật AH = EF 0,25 0,25 0,25 0,25 c c) – Chứng minh đồng dạng (c.g.c) (1) Xét ABC vuông ở A, AK là trung tuyến có: AK=KC cân ở K (2) Mà (3) Từ (1). (2), (3) có : hay tam giác AIF vuông ở I . Vậy AK vuông góc với EF 0,25 0,25 0,25 0,25 5 (0,5 điểm) Từ (1) Nhân 2 vế của (1) với rồi biến đổi được: x + y = (2) Tương tự nhân 2 vế của (1) với rồi biến đổi được: x + y = (3) Từ (2), (3) tìm được 0,25 Thay y = - x vào biểu thức A đã cho, tìm được GTNN A = 2016 khi x=2, y= -2 Vậy GTLN của A là 2016 khi x = 2, y= -2 0,25
Tài liệu đính kèm:
 de_kiem_tra_giua_hoc_ky_i_mon_toan_lop_9_nam_hoc_2020_2021_c.docx
de_kiem_tra_giua_hoc_ky_i_mon_toan_lop_9_nam_hoc_2020_2021_c.docx



