Tài liệu ôn tập và bài tập môn Toán Lớp 9 - Chuyên đề7 : Hàm số y = ax - Doãn Thị Thanh Hương
I. KIẾN THỨC CẦN NHỚ
*) Hàm số y = ax2 (a 0) có những tính chất sau:
• Nếu a > 0 thì hàm số đồng biến khi x > 0 và nghịch biến khi x <>
• Nếu a < 0="" thì="" hàm="" số="" đồng="" biến="" khi="" x="">< 0="" và="" nghịch="" biến="" khi="" x=""> 0.
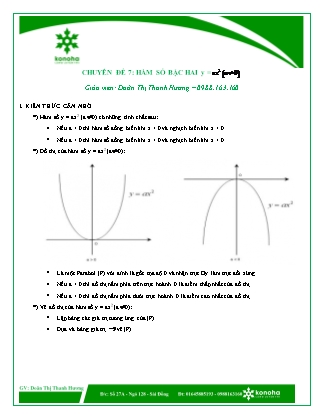
*) Đồ thị của hàm số y = ax2 (a 0):
• Là một Parabol (P) với đỉnh là gốc tọa độ 0 và nhận trục Oy làm trục đối xứng.
• Nếu a > 0 thì đồ thị nằm phía trên trục hoành. 0 là điểm thấp nhất của đồ thị.
• Nếu a < 0="" thì="" đồ="" thị="" nằm="" phía="" dưới="" trục="" hoành.="" 0="" là="" điểm="" cao="" nhất="" của="" đồ="">
*) Vẽ đồ thị của hàm số y = ax2 (a 0):
• Lập bảng các giá trị tương ứng của (P).
• Dựa và bảng giá trị vẽ (P).
II/ BÀI TẬP VẬN DỤNG.
Bài 1: Vẽ đồ thị các hàm số sau và chỉ ra khoảng đồng biến, nghịch biến của hàm số:
a) y = 2x2 b) y = - c) y = - 5x2
Bài 2: Cho hàm số . Tìm giá trị của m để:
a) Hàm số đồng biến với x <>
b) Có giá trị khi .
Bài 3: Cho parabol . Xác định m để các điểm sau nằm trên parabol:
a) b) c)
CHUYÊN ĐỀ 7: HÀM SỐ BẬC HAI y = Giáo viên: Doãn Thị Thanh Hương – 0988.163.160 I. KIẾN THỨC CẦN NHỚ *) Hàm số y = ax2 (a0) có những tính chất sau: Nếu a > 0 thì hàm số đồng biến khi x > 0 và nghịch biến khi x < 0. Nếu a 0. *) Đồ thị của hàm số y = ax2 (a0): Là một Parabol (P) với đỉnh là gốc tọa độ 0 và nhận trục Oy làm trục đối xứng. Nếu a > 0 thì đồ thị nằm phía trên trục hoành. 0 là điểm thấp nhất của đồ thị. Nếu a < 0 thì đồ thị nằm phía dưới trục hoành. 0 là điểm cao nhất của đồ thị. *) Vẽ đồ thị của hàm số y = ax2 (a0): Lập bảng các giá trị tương ứng của (P). Dựa và bảng giá trị vẽ (P). II/ BÀI TẬP VẬN DỤNG. Bài 1: Vẽ đồ thị các hàm số sau và chỉ ra khoảng đồng biến, nghịch biến của hàm số: a) y = 2x2 b) y = - c) y = - 5x2 Bài 2: Cho hàm số . Tìm giá trị của m để: a) Hàm số đồng biến với x < 0. b) Có giá trị khi . Bài 3: Cho parabol . Xác định m để các điểm sau nằm trên parabol: a) b) c) Bài 4: Xác định m để đồ thị hàm số đi qua điểm . Với m tìm được, đồ thị hàm số có đi qua điểm hay không? Đồng biến trên (0, + ∞) và nghich biến trên (- ∞, 0) Bài 5. a) Viết phương trình đường thẳng đi qua gốc toạ độ O và điểm . b) Viết phương trình parabol dạng và đi qua điểm . c) Vẽ parabol và đường thẳng trên trong cùng một hệ trục toạ độ và tìm toạ độ giao điểm của chúng. Bài 6. Cho hàm số . a) Xác định a để đồ thị hàm số đi qua điểm . b) Vẽ đồ thị hàm số vừa tìm được. c) Tìm các điểm trên đồ thị có tung độ bằng 4. d) Tìm các điểm trên đồ thị và cách đều hai trục toạ độ. Bài 7: Vẽ đồ thị (P) của hàm số và đường thẳng (d): trên cùng một hệ trục toạ độ. Xác định tọa độ giao điểm của (P) và (d) trên đồ thị.
Tài liệu đính kèm:
 tai_lieu_on_tap_va_bai_tap_mon_toan_lop_9_chuyen_de7_ham_so.doc
tai_lieu_on_tap_va_bai_tap_mon_toan_lop_9_chuyen_de7_ham_so.doc



