Tài liệu ôn tập và kiểm tra chương I môn Hình học Lớp 9 - Vũ Thanh Trọng

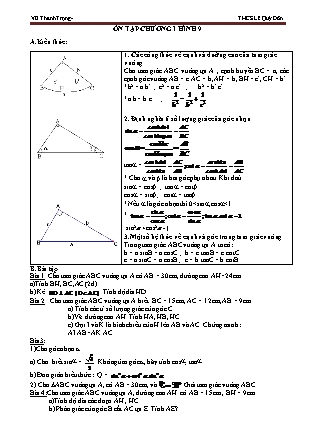
ÔN TẬP CHƯƠNG I HÌNH 9
A.Kiến thức:
1. Các công thức về cạnh và đường cao của tam giác vuông
Cho tam giác ABC vuông tại A , cạnh huyền BC = a, các cạnh góc vuông AB = c AC = b, AH = h, BH = c’, CH = b’
*b2 = a.b’ ; c2 = a.c’ ; h2 = b’.c’
*a.h = b.c ; 
2. Định nghĩa tỉ số lượng giác của góc nhọn
tana = 
* Cho a và b là hai góc phụ nhau. Khi đoù 
sina = cosb ; tana = cotb
cosa = sinb; cota = tanb
*Nếu a là góc nhọn thì 0<sina;cosa<1
* ; 
 sin2+cos2=1
3.Một số hệ thức về cạnh và góc trong tam giác vuông
Trong tam giác ABC vuông tại A ta có:
b = a.sinB = a.cosC ; b = c.tanB = c.cotC
c = a.sinC = a.cosB ; c = b.tanC = b.cotB
B.Bài tập
Bài 1. Cho tam giác ABC vuông tại A có AB = 30cm, đường cao AH=24cm
a)Tính BH, BC,AC (2đ)
b) Kẻ . Tính độ dài HD
Bài 2. Cho tam giác ABC vuông tại A biết BC = 15cm, AC = 12cm, AB = 9cm.
a) Tính các tỉ số lượng giác của góc C.
b)Vẽ đường cao AH. Tính HA, HB, HC.
c) Gọi I và K là hình chiếu của H lên AB và AC. Chứng minh: AI.AB=AK.AC
Bài3: 
1)Cho góc nhọn α
a) Cho biết sina = . Không tìm góc α, hãy tính cosa; tana 
b) Đơn giản biểu thức : Q = 
2).Cho DABC vuông tại A, có AB = 30cm, và .Giải tam giác vuông ABC
Bài 4:Cho tam giác ABC vuông tại A, đường cao AH. có AB = 15cm , BH = 9cm .
	a)Tính độ dài các đoạn AH , HC 
 	b) Phân giác của góc B cắt AC tại E. Tính AE?.
Bài 5. Bóng của một cột cờ trồng vuông góc với mặt đất dài 12m, góc nhìn của mặt trời so với phương nằm ngang của mặt đất là 350. Tính chiều cao của cột cờ.
Bài 6:Một chiếc thang dài 3m . Cần đặt chân thang cách chân tường một khoảng bằng bao nhiêu để nó tạo được với mặt đất một góc an toàn 680 . ( làm tròn đến mét )
Bài 7:	Cho tam giác ABC vuông tại A, đường cao AH. Từ trung điểm E của AC vẽ EF vuông góc với BC tại F. Chứng minh:
1) 	2) AF=BE.cosC
Bài 8:Cho tam giác ABC vuông tại A , đường cao AH. Gọi D và E là hình chiếu của H lên AB và AC Biết AB = 6cm, BC = 10cm. 
Tính BH, AH, 2) Chứng minh .
Bài 9:Cho tam giác ABC vuông tại A có AB = 15cm , AC = 20cm .
1) Tính các tỉ số lượng giác của .
2) Vẽ đường cao AH . Tính độ dài các đoạn AH , HB , HC
3) Gọi D và E lần lượt là trung điểm của BH và AH . Tia CE cắt AD tại M . 
 Chứng minh 
Bài 10:Cho tam giác ABC có ; BC= 10 cm. Tính độ dài đường cao AH.
HD:Tam giác AHB vuông tại H suy ra cotB= HB:AH
Tam giác AHC vuông tại H suy ra cotC= HC:AH
Suy ra 
Bài 11: Cho tam giác ABC có góc A bằng 1200,AB=4cm,AC=6cm.Gọi H là hình chiếu của B trên AC.
	a)Tính độ dài HA	b)Tính độ dài trung tuyến AM của tam giác ABC
HD câu b) Vẽ MF vuông góc với HC sau đó tính BH,MF,AF
Bài 12: Biết . Tính giá trị biểu thức .
Bài 13:Cho tam giác ABC có , AB = 4, AC = 6. M là trung điểm của BC. Tính độ dài đoạn thẳng AM chính xác đến 0,0001. 
 HD:Vẽ BH ^ AC và MK ^ AC. Áp dụng định lí Pi ta go cho tam giác vuông ABH:
Bài 14: Cho tam giác nhọn ABC ,hai đường cao AD và BE cắt nhau tại H, chứng minh AD=DH.tanB.tanC
Bài 15:Cho ABC vuông tại A, AB = a, AC = 3a. Trên cạnh AC lấy các điểm D, E sao cho AD = DE = EC.
	a) Chứng minh .	b) Chứng minh đồng dạng CDB.
	c) Tính tổng .
	ĐS: a) 	c) .
Bài 16:Cho tam giác ABC vuông tại A, đường cao AH. Gọi D là điểm đối xứng với A qua điểm B. Trên tia đối của tia HA lấy điểm E sao cho HE = 2HA. Gọi I là hình chiếu của D trên HE.
	a) Tính AB, AC, HC, biết AH = 4cm, HB = 3cm.	b) Tính .
	c) Chứng minh .	d) Chứng minh: .
	ĐS: a) , , 	b) 
	d) .
KIỂM TRA CHƯƠNG I HÌNH HỌC 9
Thời gian làm bài: 45 phút
ĐỀ BÀI:
Câu 1: (2 điểm) :Giải ∆ABC ( ) biết BC = 20cm , 
Câu 2: (1,5 điểm) Bóng của một cột cờ trồng vuông góc với mặt đất dài 12m, góc nhìn của mặt trời so với phương nằm ngang của mặt đất là 350. Tính chiều cao của cột cờ.
Câu 3(2đ): 
a) Cho góc nhọn a, biết: Không tính số đo góc α. Hãy tính cosa ; tana.
b)Rút gọn biểu thức: A=
Câu 4: (4,5 điểm) 
Cho tam giác ABC vuông tại A, đường cao AH. có AB = 15cm , BH = 9cm .
a)Tính độ dài các đoạn AH , HC 
 b) Kẻ trung tuyến AM.(MBC).Tính diện tích tam giác AHM
c) Kẻ HEAB (EAB),HDAM (DAM).Chứng minh ED= HA sin
 (Độ dài cạnh làm tròn đến chữ số thập thứ hai )
KIỂM TRA CHƯƠNG I HÌNH HỌC 9
Thời gian làm bài: 45 phút
ĐỀ BÀI:
Câu 1. (2 điểm) Cho tam giác ABC vuông tại A,đường cao AH, có AB = 9cm, BH =5,4cm. Tính BC, AH, AC.
Câu 2. (2điểm) Cho góc nhọn , biết , không tính số đo góc . 
Hãy tính ;;
Câu 3.(1,5điểm) Tượng đài chiến thắng là một công trình kiến trúc độc đáo được thi công nhằm kỷ niệm ngày giải phóng thị xã Long Khánh, ngày 21 – 4 – 1975 – thể hiện ý chí quyết thắng của quân và dân ta. 
Em hãy tính chiều cao của công trình này biết rằng khi tia nắng của mặt trời tạo với mặt đất một góc 520 thì bóng của nó trên mặt đất là 16m. 
(Giả sử chu vi mặt đáy của khối chóp tam giác không đáng kể)
Bài 4.(3,5 điểm) Cho tam giác nhọn ABC có AC = 8cm,kẻ đường cao AH.
a) Giải tam giác AHC.
b) Tia phân giác của cắt AH tại I. Tính diện tích tam giác AIC?
Bài 5.(1,0điểm) Cho tam giác nhọn ABC ,hai đường cao AD và BE cắt nhau tại H, chứng minh AD=DH.tanB.tanC
 ..Hết ..