Bài giảng Hình học Lớp 9 - Tiết 40: Góc nội tiếp

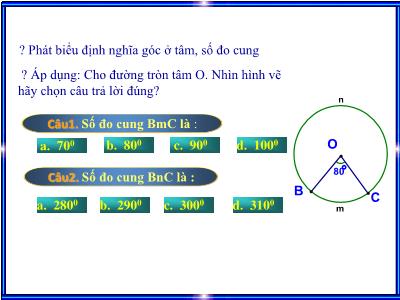
? Phát biểu định nghĩa góc ở tâm, số đo cung ? Áp dụng: Cho đường tròn tâm O. Nhìn hình vẽ hãy chọn câu trả lời đúng?b. 800 a. 700 c. 900 d. 1000 b. 2900 a. 2800 c. 3000 d. 3100 Câu1. Số đo cung BmC là :Câu2. Số đo cung BnC là :80°nmOBC Hình 1Hình 2Hình 1 là hình ảnh lá quốc kì Việt Nam. Em hãy tìm cách vẽ ngôi sao có 5 cách đều như hình 280°nmOBCATiết 40: Góc nội tiếp Góc xAy có: + đỉnh nằm trên đường tròn;+ hai cạnh chứa hai dây cung của đường tròn đó.là góc nội tiếp OBCA1- Định nghĩa :Góc nội tiếp là góc có đỉnh nằm trên đường tròn hai cạnh chứa hai dây cung của đường tròn đóGãc néi tiÕp :§Ønh n»m trªn đường trßnHai c¹nh chøa hai d©y cña đường trßn103254687109103254687109CBOA1. Định nghĩa: Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó. Cung nằm bên trong góc được gọi là cung bị chắn.CBOABCOABCOA là cung bị chắn. là góc nội tiếp.ABCOCÁCH VẼ HÌNH:Hình 13aHình 13b1. Định nghĩa (SGK-72)là góc nội tiếp chắna)b)Hình 13Tiết 40: Góc nội tiếplà góc nội tiếp chắna)Ob)Oc)Od)OOa)Ob)Hình 14Hình 15?1: Vì sao các góc ở hình 14 và hình 15 không phải là góc nội tiếp?Tiết 40: Góc nội tiếp1. Định nghĩa (SGK-72)Hình 16Hình 17Hình 18OABCABCDa) Tâm O nằm trên một cạnh của góc BAC(h.16)b)Tâm O nằm bên trong góc BAC (h.17)c)Tâm O nằm bên ngoài góc BAC( h.18)2. Định lí: Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo cung bị chắn.Chứng minh .- Tâm đường tròn nằm trên một cạnh của góc.- Tâm đường tròn nằm bên trong góc.- Tâm đường tròn nằm bên ngoài góc.Ta phân biệt ba trường hợp:OABCOGTKLBAC : gãc néi tiÕp (O)BAC = s® BC1. Định nghĩa (SGK – 72)là góc nội tiếp chắn 2. Định lí (SGK – 73)là góc nội tiếp chắn Tiết 40: Góc nội tiếp3. Hệ quả: Trong một đường tròn:Các góc nội tiếp bằng nhau chắn các cung bằng nhau .b) Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.c) Góc nội tiếp (nhỏ hơn hoặc bằng 900) có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.d) Góc nội tiếp chắn nửa đường tròn là góc vuông.ABCA'ABCDEFOABCBCOA1. Định nghĩa (SGK – 72)là góc nội tiếp chắn 2. Định lí (SGK – 73)là góc nội tiếp chắn Tiết 40: Góc nội tiếp3. Hệ quả (SGK – 74) Góc nội tiếpBµi tËp : Cho h×nh vÏ.0AMNBBiÕt s® MN = 1000 ®iÒn vµo dÊu 1) MAN = . s® = 2) MBN = sđ 3) AMN = 4) MON = 500= 500 900= 1000MN MN s® AN = s® MNĐÁP ÁNMENUCho hình vẽ. Tính số đo ABCĐÁP ÁN ĐÚNG B	A. 60 C.120 B. 90 D.180 OACBD 25 độĐÁP ÁNA	 100 độB 75 độ C	 50 độ	Trong một đường tròn, nếu số đo cung bị chắn bằng 50 độ thì số đo góc nội tiếp chắn cung đó là bao nhiêu?ĐÁP ÁN ĐÚNG 	DMENUĐÁP ÁNTrong một đường tròn, hai góc nội tiếp cùng chắn một cung thì bằng nhau.	Bài tập: Khẳng định sau đây đúng hay sai?ĐÁP ÁN ĐÚNG Đúng 	MENUĐÁP ÁNA. MBN= , PCQ= Cho MAN = . Tính số đo góc MBN và PCQ ? (hình vẽ sau)MENUB. MBN= , PCQ= C. MBN= , PCQ= D. MBN= , PCQ= ĐÁP ÁN ĐÚNG C	B, D, C thẳng hàng=>=>=>=>góc ADC + góc ADB = 1800góc ADC = 900 ; góc ADB = 900Góc nội tiếp chắn nửa đtròn* Sơ đồ phân tíchLời giải:+) Có góc ADC là góc nội tiếp chắn nửa (O) đường kính ACgóc ADC = 900 ( Hệ quả góc nội tiếp) (1)+) Có góc ADB là góc nội tiếp chắn nửa (O/) đường kính ABgóc ADB = 900 ( Hệ quả góc nội tiếp) (2)+) Từ (1) và (2) =>Góc BDC = 1800 góc ADC + góc ADB = 1800Nên C, B, D thẳng hàngGóc BDC = 1800=>Bài 20 (sgk-76): Cho 2 đường tròn (O) và (O/) cắt nhau tại A và D.Vẽ các đường kính AC và AB của 2 đường tròn đó. Chứng minh 3 điểm B, C, D thẳng hàng. ∆BMN cân tại B=>cung AmB = cung ANB*Sơ đồ phân tíchGóc BMN = góc BNM=>Hai đtròn (O) và (O’) bằng nhau (gt)Bài 21 (sgk-76): Cho 2 đường tròn bằng nhau (O) và (O/) cắt nhau tại A và B.Vẽ đường thẳng đi qua A cắt (O) tại M và cắt (O’) tại N (A nằm giữa M và N). Hỏi tam giác MBN là tam giác gì? Tại sao? => Bài tập: Cho nửa đường tròn đường kính AB lấy điểm C trên cung AB sao cho cung AC có số đo bằng 600. So sánh các góc của tam giác ABCGọi M, N lần lượt là điểm chính giữa của các cung AC và BC. Hai dây AN và BM cắt nhau tại I. Chứng minh tia CI là tia phân giác của góc ACB. Bài tập: HƯỚNG DẪN VỀ NHÀ:Học kĩ nội dung bàiBTVN: 16;17;18; 19;22;23;24;25 (sgk-75)Chuẩn bị: Góc tạo bởi tia tiếp tuyến và dây cung