Đề kiểm tra học kỳ I môn Toán Lớp 9 - Năm học 2015-2016 - Trần Ngọc Minh

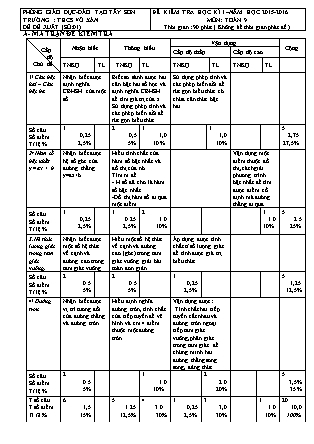
PHÒNG GIÁO DỤC-ĐÀO TẠO TÂY SƠN
TRƯỜNG : THCS VÕ XÁN 
ĐỀ ĐỀ XUẤT (SỐ:01)
ĐỀ KIỂM TRA HỌC KÌ I –NĂM HỌC 2015-2016 
MÔN: TOÁN 9 
Thời gian : 90 phút ( Không kể thời gian phát đề )
A- MA TRẬN ĐỀ KIỂM TRA 
 Cấp 
 độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
TNKQ
TL
TNKQ
TL
TNKQ
TL
TNKQ
TL
1/ Căn bậc hai – Căn bậc ba 
Nhận biết được định nghĩa CBHSH của một số
Biết so sánh được hai căn bậc hai số học và định nghĩa CBHSH để tìm giá trị của x.
Sử dụng phép tính và các phép biến đổi để rút gọn biểu thức 
Sử dụng phép tính và các phép biến đổi để rút gọn biểu thức có chứa căn thức bậc hai 
Số câu
Số điểm
Tỉ lệ %
1
0,25 
2,5%
2
0,5 
5%
1
1,0 
 10%
1
1,0 10%
5
 2,75
 27,5%
2/ Hàm số bậc nhất 
y =ax + b
Nhận biết được hệ số góc của đường thẳng y=ax+b 
Hiểu tính chất của hàm số bậc nhất và đồ thị của nó 
Tìm m để
- H số đã cho là hàm số bậc nhất 
-Đồ thị hàm số đi qua một điểm 
Vận dụng một điểm thuộc đồ thị,cách giải phương trình bậc nhất để tìm được điểm cố định mà đường thẳng đi qua. 
Số câu
Số điểm
Tỉ lệ %
1
0,25 
2,5%
1
0.25 
2,5%
2
1.0 
10%
1
1.0 
10%
5
2.5
25%
3.Hệ thức lượng giác trong tam giác vuông. 
Nhận biết được một số hệ thức về cạnh và đường cao trong tam giác vuông 
Hiểu một số hệ thức về cạnh và đường cao (góc) trong tam giác vuông giải bài toán đơn giản 
Áp dụng được tính chất tỉ số lượng giác để tính được giá trị biểu thức 
Số câu
Số điểm
Tỉ lệ %
2
0.5 
5%
2
0.5 
5%
1
0,25 
 2,5%
5
 1,25
12,5%
4/ Đường tròn
Nhận biết được vị trí tương đối của đường thẳng và đường tròn . 
Hiểu định nghĩa đường tròn, tính chất của tiếp tuyến để vẽ hình và cm 4 điểm thuộc một đường tròn 
Vận dụng được:
 Tính chất hai tiếp tuyến cắt nhau và đường tròn ngoại tiếp tam giác vuông,phân giác trong tam giác để chứng minh hai đường thẳng song song, đảng thức 
Số câu
Số điểm
Tỉ lệ %
2
0.5 
5%
1
1.0
 10%
2
2.0
20%
5
 3,5%
35%
T số câu
T số điểm
Tỉ lệ %
6
1,5 
15%
5
1.25
12,5%
4
 3.0
30%
1
0,25 
 2,5%
3
3,0 
30%
1
1.0
10%
20
10,0 
100%
B- ĐỀ KIỂM TRA 
 I. Phần trắc nghiệm (3,0 điểm)
Bài 1 (2 điểm): Chọn đáp án đúng và ghi vào phần bài làm 
Câu 1. Căn bậc hai số học của 9 là 
	A. 3	B. 9	C. – 9 	D. – 3 và 3
Câu 2. So sánh 9 và , ta có kết luận sau:
A. . B. . C. . D. Không so sánh được.
Câu 3. Hệ số góc của đường thẳng y = 1 -2x là 
	A. 2x	B. -2x	C. 2	D. – 2
Câu 4 Cho hàm số , kết luận nào sau đây đúng ?
A.Hàm số luôn đồng biến . 
B.Đồ thị hàm số luôn đi qua gốc toạ độ.
C.Đồ thị cắt trục hoành tại điểm có hoành độ bằng 8.
D.Đồ thị cắt trục tung tại điểm có tung độ bằng-4.
Câu 5.Nếu thì x bằng
 A. 2. B. 64. C. 25. D. 4.
Câu 6.Tam giác ABC vuông ở A có AB = 6cm, BC = 10cm. Độ dài đường cao AH bằng:
	A. 24cm	B. 48cm	C. 4,8cm 	D. 2,4cm
Câu 7:Cho tam giác ABC vuông tại A, có AB = 6cm, = 300. độ dài cạnh BC là:
A . 12 cm. 	B. cm	 C. 10 cm. 	 D. 6 cm.
Câu 8.Giá trị của biểu thức bằng
A. 1. B. 2. C. 3. D. 0.
Bài 2 ( 1 điểm) Hãy nối mỗi ý ở cột A với một ý ở cột B để được khẳng định đúng.
A
B
1.Trong một tam giác vuông, bình phương mỗi cạnh góc vuông bằng
A.Tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền.
2.Trong một tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng
B.Tích của cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền 
3. Nếu đường thẳng a và đường tròn (O; R) cắt nhau
C.Thì d = R. (d là khoảng cách từ O đến a).
4. Nếu đường thẳng a và đường tròn (O; R) tiếp xúc nhau
D.Thì d < R. (d là khoảng cách từ O đến a).
E.Thì d > R. (d là khoảng cách từ O đến a).
 II. Phần tự luận (7,0 điểm): 
Bài 1 (2,0 điểm): Rút gọn các biểu thức:
a) 	 b) (với )
Bài 2 (2,0 điểm): Cho hàm số : y = (m+1)x + m -1 . (d) (m là tham số)
Xác định m để hàm số đã cho là hàm số bậc nhất.
Xác đinh m để đồ thị hàm số đã cho đi qua điểm ( 7 ; 2).
 c) Chứng tỏ (d) đã cho luôn đi qua một điểm cố định khi m thay đổi 
Bài 3 (3,0 điểm): Cho nửa (O; R) đường kính AB. Vẽ tiếp tuyến Ax (Ax và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB), trên tia Ax lấy điểm P (AP > R). Vẽ tiếp tuyến PE với nửa đường tròn (E là tiếp điểm), đường thẳng PE cắt AB tại F.
Chứng minh :4 điểm P, A, E, O cùng thuộc một đường tròn.
Chứng minh : PO // BE.
Qua O kẻ đường thẳng vuông góc với OP cắt PF tại M.Chứng minh : EM.PF = PE.MF
 Hết 
C- HƯỚNG DẪN CHẤM 
I. Phần trắc nghiệm (3,0 điểm): 
 Chọn đúng mỗi câu hoặc nối đúng mỗi cột ghi 0,25 điểm.
Câu
1
2
3
4
5
6
7
8
1-->B
2-->A
3-->D
4-->C
Đáp án
A
C
D
C
B
C
A
B
II. Phần tự luận (7,0 điểm): 
Bài
(điểm)
Đáp án
Thang điểm
Bài 1
(2,0đ)
a) Rút gọn (1,0đ):
 =
0,5đ
 = 
0,5đ
b) Rút gọn (1,0đ):
0,5đ
 =
0,25đ
 = 0
0,25đ
Bài 2
(2,0đ)
a) Để hàm số đã cho là hàm bậc nhất thì: 
0,5đ
b) Để đồ thị hàm số đã cho đi qua điểm (7;2) thì:
0,25đ
0,25đ
c)Gọi I(a;b) là điểm cố định mà đồ thị hàm số (d) đi qua 
Vì I(a;b) thuộc đồ thị hàm số (d) nên ta có
 b=(m+1)a+m-1
 m(a+1)+a-b-1=0
(d) đi qua điểm cố định I với mọi m
a+1=0 và a-b-1=0
a= -1; b= -2
 I(-1;-2) 
Điều này chứng tỏ (d) luôn luôn đi qua điểm cố định I(-1; -2) với mọi giá trị của m
0,25đ
0,25 đ
0,25đ
0,25đ
Bài 3
(3,0 đ)
 Vẽ hình đúng 
0.25đ
a) Chứng minh 4 điểm P;A;E;O cùng thuộc một đường tròn (0,75 điểm)
Ta có :PA OA ( tính chất tiếp tuyến)
 và :PE OE (tính chất tiếp tuyến)
0.25đ
0.25đ
 P, A, O, E cùng thuộc một đường tròn đường kính PO
0.25đ
b) Chứng minh PO//BE (1,0 điểm)
Ta có : PA = PE ( tính chất hai tiếp tuyến cắt nhau)
 và : OA = OE (bán kính)
0.25đ
 OP là đường trung trực của AE (1). 
0.25đ
Vì E thuộc đường tròn đường kính AB (giả thiết)
 (2)
0.25đ
Từ (1) và (2) ta có OP // BE
0.25đ
c) Chứng minh EM.PF=PE.MF ( 1,0 điểm)
Chứng minh được OM là phân giác trong của 
0.25đ
 (3)
0.25đ
OP là phân giác ngoài tại O của (4) 
0.25đ
Từ (3) và (4) ta có 
0.25đ
 Ghi chú: 
Bài 3 ( Phần tự luận) chỉ chấm điểm khi có hình vẽ đúng 
Mọi cách giải khác mà đúng và phù hợp đều ghi điểm tối đa
Điểm toàn bài được làm tròn một chữ số thập phân theo nguyên tắc làm tròn số 
 Hết 
 Phú Phong, ngày 02 tháng 12 năm 2015
 Giáo viên ra đề 
 TRẦN NGỌC MINH