Đề thi học sinh giỏi môn Toán Lớp 9 (có đáp án)
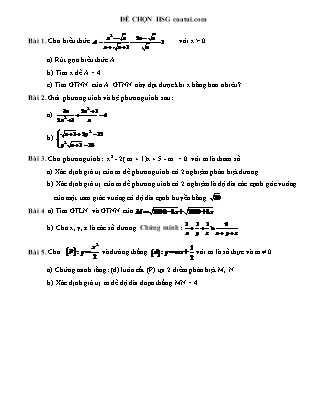
Bài 1. Cho biểu thức với x > 0
a) Rút gọn biểu thức A
b) Tìm x để A = 4
c) Tìm GTNN của A. GTNN này đạt được khi x bằng bao nhiêu?
Bài 2. Giải phương trình và hệ phương trình sau:
a)
b)
Bài 3. Cho phương trình: x2 - 2( m + 1)x + 5 - m = 0 với m là tham số.
a) Xác định giá trị của m để phương trình có 2 nghiệm phân biệt dương.
b) Xác định giá trị của m để phương trình có 2 nghiệm là độ dài các cạnh góc vuông
của một tam giác vuông có độ dài cạnh huyền bằng .
Bài 4. a) Tìm GTLN và GTNN của
b) Cho x, y, z là các số dương. Chứng minh:
Bài 5. Cho và đường thẳng với m là số thực và m 0
a) Chứng minh rằng: (d) luôn cắt (P) tại 2 điểm phân biệt M, N.
b) Xác định giá trị m để độ dài đoạn thẳng MN = 4
ĐỀ CHỌN HSG cuatui.com Bài 1. Cho biểu thức với x > 0 a) Rút gọn biểu thức A b) Tìm x để A = 4 c) Tìm GTNN của A. GTNN này đạt được khi x bằng bao nhiêu? Bài 2. Giải phương trình và hệ phương trình sau: a) b) Bài 3. Cho phương trình: x2 - 2( m + 1)x + 5 - m = 0 với m là tham số. a) Xác định giá trị của m để phương trình có 2 nghiệm phân biệt dương. b) Xác định giá trị của m để phương trình có 2 nghiệm là độ dài các cạnh góc vuông của một tam giác vuông có độ dài cạnh huyền bằng . Bài 4. a) Tìm GTLN và GTNN của b) Cho x, y, z là các số dương. Chứng minh: Bài 5. Cho và đường thẳng với m là số thực và m ¹ 0 a) Chứng minh rằng: (d) luôn cắt (P) tại 2 điểm phân biệt M, N. b) Xác định giá trị m để độ dài đoạn thẳng MN = 4 HDG CHON HSG cuatui.com. Bài 1. Cho biểu thức với x > 0 a) b) A = 4 c) GTNN của A là Bài 2. Giải phương trình và hệ phương trình sau: a) đk x ¹ 0 Đặt (1) thay vào pt ta có: ( 2) Giải (2) ta được: + Với t = 1 , ta có ( vô nghiệm) + Với t = , ta có: Giải được x1 =1; x2 = 1/2 b) Đặt a= thay vào hệ ta có; giải hệ ta được + Với ( a =4, b = 8) Ta có giải hệ ta được + Với ( a =8, b =4) Ta có giải hệ ta được Vậy hpt có 4 nghiệm: Bài 3. Cho phương trình: x2 - 2( m + 1)x + 5 - m = 0 với m là tham số. a) Phương trình có 2 nghiệm phân biệt dương. b) vì x1, x2 là độ dài 2 cạnh góc vuông của một tam giác vuông có độ dài cạnh huyền bằng . Þ x12 + x22 = 30 Û S2 - 2P - 30 =0 Û 2m2 + 5m -18 = 0. Giải ra được m= 2 hoặc m = -9/2 ( loại) Bài 4. a) Tìm GTLN và GTNN của Điều kiện: + Áp dụng dấu " = " xảy ra khi A= 0 hoặc B= 0 Do đó , dấu " =" xảy ra khi hoặc Vậy GTNN của M = khi hoặc + Áp dung BĐT Bu-nhi-a-cop- ki với mọi số a, b, x, y ta có ( a2 + b2 )( x2 + y2 ) ≥ ( ax + by)2 Do đó: , dấu "=" xảy ra khi 2008-3x= 2009+3x Vây GTLN của M = b) Cho x, y, z là các số dương. Chứng minh: Áp dụng Cosi cho 3 số dương, ta có ( 1) (2) Nhân (1) với (2) Bài 5. và a) Phương trình hoành độ giao điểm: x2 - 2mx - 1 = 0 (1) D' = m2 + 1 > 0 nên pt có 2 nghiệm phân biệt. Do đó đường thẳng (d) cắt (P) tại 2 điểm phân biệt M, N. b) Gọi M( x1; y1), N(x2; y2). Ta có: = 4 (x2 - x1 )2 + (y2 - y1 )2 = 16 (y2 - y1 )2 = 16 - (x2 - x1 )2 (x2 - x1 )2 = 16 - (x2 - x1 )2 2 (x2 - x1 )2 = 16 * Mà và (x2 - x1 )2 = ( x1 + x2)2 - 4x1.x2 thay vào * Ta được: 2( 4m2 + 4 ) = 16 => 4m2 + 4 = 8 => 4m2 = 4 => m2 = 1 Vậy m = 1; m = -1.
Tài liệu đính kèm:
 de_thi_hoc_sinh_gioi_mon_toan_lop_9_co_dap_an.doc
de_thi_hoc_sinh_gioi_mon_toan_lop_9_co_dap_an.doc



