Bộ 10 đề ôn tập chương I môn Hình học Lớp 9 (có đáp án)
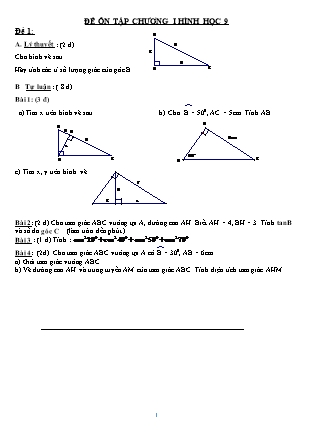
Bài 1: (3,5 đ)
a) Tìm x trên hình vẽ sau
b) Cho , AC= 5cm. Tính AB
c) Tìm x, y trên hình vẽ
Bài 2 : ( 1 đ) Tính :
Bài 3 : (4,5 điểm). Cho tam giác ABC vuông tại A, đường cao AH, AB = 3cm,
BC = 6cm. 1/ Giải tam giác vuông ABC
2/ Gọi E, F lần lượt là hình chiếu của H trên cạnh AB và AC:
a/ Tính độ dài AH và chứng minh: EF = AH.
b/ Tính: EA EB + AF FC
Bài 4: (1 điểm) Biết sin = 23 . Tính giá trị của biểu thức: A = 2sin2 + 5cos2 .
Bạn đang xem tài liệu "Bộ 10 đề ôn tập chương I môn Hình học Lớp 9 (có đáp án)", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
ĐỀ ÔN TẬP CHƯƠNG I HÌNH HỌC 9 Đề 1: A. Lý thuyết : (2 đ) Cho hình vẽ sau Hãy tính các tỉ số lượng giác của góc B. B. Tự luận : ( 8 đ) Bài 1: (3 đ) a) Tìm x trên hình vẽ sau b) Cho B = 500, AC = 5cm. Tính AB c) Tìm x, y trên hình vẽ Bài 2: (2 đ) Cho tam giác ABC vuông tại A, đường cao AH. Biết AH = 4, BH = 3. Tính tanB và số đo góc C (làm tròn đến phút ). Bài 3 : (1 đ) Tính : Bài 4: (2đ) Cho tam giác ABC vuông tại A có B = 300, AB = 6cm a) Giải tam giác vuông ABC. b) Vẽ đường cao AH và trung tuyến AM của tam giác ABC. Tính diện tích tam giác AHM. Đề 2: Bài 1: (3,5 đ) a) Tìm x trên hình vẽ sau b) Cho , AC= 5cm. Tính AB c) Tìm x, y trên hình vẽ Bài 2 : ( 1 đ) Tính : Bài 3 : (4,5 điểm). Cho tam giác ABC vuông tại A, đường cao AH, AB = 3cm, BC = 6cm. 1/ Giải tam giác vuông ABC 2/ Gọi E, F lần lượt là hình chiếu của H trên cạnh AB và AC: a/ Tính độ dài AH và chứng minh: EF = AH. b/ Tính: EAEB + AFFC Bài 4: (1 điểm) Biết sin a = . Tính giá trị của biểu thức: A = 2sin2 a + 5cos2 a. Đề 3: Bài 1: (3,5 đ) a) Tìm x trên hình vẽ sau b) Cho , AC= 5cm. Tính AB c) Tìm x, y trên hình vẽ Bài 2 : ( 1đ) Sắp xếp theo thứ tự tăng dần: tg230, cotg 710, tg260 , cotg 400 , tg 170 , cotg 500 Bài 3: (4,5 điểm). Cho tam giác ABC vuông tại A, đường cao AH, AB = 3cm, BC = 6cm. 1/ Giải tam giác vuông ABC 2/ Gọi E, F lần lượt là hình chiếu của H trên cạnh AB và AC: a/ Tính độ dài AH và chứng minh: EF = AH. b/ Tính: EAEB + AFFC Bài 2: (1 điểm). Cho sin = 0,6. Hãy tính tan Đề 4: Bài 1: (3 đ) a) Tìm x trên hình vẽ sau b) Cho , AC= 5cm. Tính AB c) Tìm x, y trên hình vẽ Bài 2 : ( 1 đ) : Sắp xếp theo thứ tự tăng dần: sin 270, cos 780, sin190 , cos 680 , sin 540 , cos 500. Bài 3: (4,5 điểm). Cho tam giác ABC vuông tại A, đường cao AH, AB = 3cm, BC = 6cm. 1/ Giải tam giác vuông ABC 2/ Gọi E, F lần lượt là hình chiếu của H trên cạnh AB và AC: a/ Tính độ dài AH và chứng minh: EF = AH. b/ Tính: EAEB + AFFC Bài 4: (1 điểm). Biết sin2 = . Tính cos; tg Đề 5: Bài 1: (3 đ) a) Tìm x trên hình vẽ sau b) Cho , AC= 5cm. Tính AB c) Tìm x, y trên hình vẽ Bài 2 : ( 1 đ) : Rút gọn biểu thức: Bài 3: (4,5 điểm). Cho tam giác ABC vuông tại A, đường cao AH, AB = 3cm, BC = 6cm. 1/ Giải tam giác vuông ABC 2/ Gọi E, F lần lượt là hình chiếu của H trên cạnh AB và AC: a/ Tính độ dài AH và chứng minh: EF = AH. b/ Tính: EAEB + AFFC Bài 4: (1 điểm) Cho . Tính giá trị của biểu thức A = Đề 6: Câu 1 : Döïng goùc nhoïn bieát cos = Câu 2: Tam giác ABC vuông ở A có đường cao AH (HBC). Biết BH=1cm, AH=3cm tính số đo của góc ACB ( làm tròn đến độ). Câu 3 : Cho ABC vuông tại A , = 600 , độ dài đường cao AH = 5 cm, tínhAC . Câu 4 : Sắp xếp theo thứ tự tăng dần: sin 250, cos 800,sin160 ,cos 700 , sin 550 , cos 500. Câu 5: ChoABC vuông tại A .Biết AB = 16cm,AC =12cm.Tính SinB,CosB. Câu 6: Rút gọn biểu thức: Câu 7: Tính Giá trị biểu thức : Câu 8: Cho ABC vuông tại A , AH BC . Biết CH =9cm,AH =12cm. Tính độ dài BC, AB, AC. Câu 9: Cho ABC vuông tại A , AH BC . Biết BH =3,6cm,CH =6,4cm. Tính chu vi ABC Câu 10: Cho ABC vuông tại A , AH BC. Vẽ HD AB (D AB) , vẽ HEAC (E AC) .Biết BH = 9cm, CH = 16cm. Tính DE Đề 7: I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (3 điểm) Khoanh tròn vào kết quả đúng nhất trong các câu sau: Câu 1 : Cho , A = 900 , B = 580, cạnh a = 72 cm. Độ dài của cạnh b bằng : A. 59cm B. 60cm C. 61cm D. Một đáp số khác Câu 2 : Hai cạnh của một tam giác là 8 và 12cm, góc xen giữa hai cạnh đó bằng 300. Diện tích của tam giác này là: A. 95cm2 B. 96cm2 C. 97cm2 D. Một đáp số khác Bài 3 : Biết tg= 0,1512. Số đo góc nhọn là : A. 8034’ B. 8035’ A. 8036’ D. Một đáp số khác Bài 4 : Trong các câu sau, câu nào sai : A. sin200 cos400 C. cos400 > sin200 D. cos200 > sin350 Bài 5 : Cho tam giác ABC vuông ở A. BC = 25 ; AC = 15 , số đo của góc C bằng: A. 530 B. 520 C. 510 D. 500 Bài 6 : Cho tam giác ABC, đường cao AH. Hệ thức nào sau đây là điều kiện đủ để tam giác ABC vuông tại A. Câu nào sau đây đúng: A. B. C. D. cả A, B, C đều đúng II. PHẦN TỰ LUẬN ( 7điểm) Bài 1( 2điểm) Không dùng bảng số và máy tính hãy tính: a) tg830 – cotg 70 b) sin.cos Biết tg+cotg = 3 Bài 2 (2 điểm) :Tính chiều cao của một cột tháp, biết rằng lúc mặt trời ở độ cao 500 ( nghĩa là tia sáng của mặt trời tạo với phương nằm ngang của mặt đất một góc bằng 500) thì bóng của nó trên mặt đất dài 96m Bài 3 ( 3 điểm) : Cho hình thang cân ABCD ( AB//CD và AB < CD), BC = 15cm ; Đường cao BH = 12cm, DH = 16cm a) Chứng minh DB vuông góc với BC b) Tính diện tích hình thang ABCD c) Tính BCD (làm tròn đến độ) Đề 8: I. PHẦN TRẮC NGHIỆM: (3.0 điểm) Câu 1: Dựa vào hình 1. Hãy chọn câu đúng nhất: BA2 = BC. CH B) BA2 = BC. BH C) BA2 = BC2 + AC2 D) Cả 3 ý A, B, C đều sai. Câu 2: Dựa vào hình 1. Độ dài của đoạn thẳng AH bằng: A) AB.AC B) BC.HB C) D) BC.HC Câu 3: Dựa vào hình 1. Hãy chọn câu đúng nhất: A) B) C) D) Cả ba câu A, B, C đều sai Câu 4: Hãy chọn câu đúng nhất ? A) sin370 = sin530 B) cos370 = sin530 C) tan370 = cot370 D) cot370 = cot530 Câu 5: Cho DABC vuông tại A. Câu nào sau đây đúng và đầy đủ nhất ? A) AC = BC.sinC B) AB = BC.cosC C) Cả hai ý A và B đều đúng . D) Cả hai ý A và B đều sai . Câu 6: Dựa vào hình 2. Hãy chọn đáp đúng nhất: A) cos= B) sin= C) tan= D) cot= II.PHẦN TỰ LUẬN: (7.0 điểm) Bài 1: (2 điểm) Cho DABC vuông tại A, có AB = 30cm, và C = 300. Giải tam giác vuông ABC. Bài 2: (3 điểm) Cho DABC vuông tại A, đường cao AH. Biết HB = 3,6cm ; HC = 6,4cm. Tính độ dài các đoạn thẳng: AB, AC, AH. Kẻ HEAB ; HFAC. Chứng minh rằng: AB.AE = AC.AF. Bài 3: (1 điểm) Cho là góc nhọn. Rút gọn biểu thức: A = sin6+ cos6 + 3sin2 – cos2 Bài 4: (1 điểm) Cho DABC vuông tại A, đường cao AH. Cho biết BH = a ; HC = b. Chứng minh rằng: Đề 9: I/ Trắc nghiệm: (2 điểm) Câu1: sin 590 – cos310 bằng A. sin 280 B. cos 280 C. 0 D. 0,5 Câu 2: Cho cos= 0,8 khi đó A. tan- sin = 0,15 B. tan= 0,6 C. cot= 0,75 D. sin= 0,75 Câu 3: Cho + = 900, ta có A. sin = sin B.tan= C. sin2+ cos2 = 1 D. tan. cot= Câu 4: Cho tam giác vuông cân ABC đỉnh A có BC = 6cm, khi đó AB bằng A.cm B. cm C.36 cm D. cm II. Tự luận: (8 điểm) Câu 1:(7 điểm) Cho tam giác ABC có AB = 6 cm , AC = 8 cm, BC = 10 cm. a, Chứng minh tam giác ABC vuông. b, Từ A hạ AH BC ( H BC ). Gọi M, N lần lượt là hình chiếu của H trên AB và AC. Tính BH và MN c, Tính diện tích tứ giác MHNA. d, Chứng minh góc AMN bằng góc ACB. Câu 2:(1 điểm). Cho tam giác ABC nhọn. Chứng minh rằng: AB2 = AC2 + BC2 – 2 AC.BC. cosC Đề 10: I- TRAÉC NGHIEÄM:(2 ñieåm) Khoanh troøn chöõ caùi ñöùng tröôùc keát quaû maø em choïn: Câu 1: Cho tam giác ABC vuông tại A (hình 1). Khi đó đường cao AH bằng: A. 6,5 B. 6 C. 5 D. 4,5 Câu 2: Trong hình 1, độ dài cạnh AC là: A. 13 B. C. 2 D. 3 Câu 3: Cho tam giác ABC vuông tại A, đường cao AH (Hình 2) , hệ thức nào sau đây là đúng A . cosC = B. tg B = Hình 2 C. cotgC = D. cotgB = Câu 4: Tìm x trong tam giác ABC vuông tại A, đường cao AH (H.3) A. x = 8 B. x = 4 C. x = 8 D. x = 2 H.3 Câu 5: Cho tam giác ABC vuông tại A có BC = 5cm, C = 300 (hình 4), trường hợp nào sau đây là đúng: A/ AB = 2,5 cm B/ AB = cm C/ AC = cm D/ AC = 5 cm. H.4 Câu 6. Cho một tam giác vuông có hai góc nhọn là α và β (Hình 3 bên dưới). Biểu thức nào sau đây không đúng? A. sinα = cosβ B. cotα = tanβ C. sin2α + cos2β =1 D. tanα = cotβ II. TỰ LUẬN Bài 1. (2 điểm)Tính x, y, h trong hình dưới đây Bài 2 (1,5điểm)Trong tam giác ABC có AC = 10 cm ; đường cao AH. Hãy tính độ dài AH , AB. Bài 3 (3.5 điểm) Cho tam giaùc ABC coù AC = 3cm, AB = 4cm, BC=5cm a) Chöùng minh tam giaùc ABC vuoâng, tính caùc goùc B, C ? b) Phaân giaùc cuûa caét BC taïi D. Tính BD, CD c) Töø D keû DE vaø DF laàn löôït vuoâng goùc vôùi AB, AC. Töù giaùc AEDF laø hình gì? Tính chu vi cuûa töù giaùc AEDF? Đáp án đề 1 A. Lý thuyết : (2 đ) Hãy tính các tỉ số lượng giác của góc B. Tính đúng mỗi tỉ số lượng giác được 0,5 điểm B. Tự luận : ( 8 đ) Bài 1: (3 đ) mỗi câu đúng 1 điểm a) Tìm x trên hình vẽ sau x2 = 4.9 => x = 6 b) Cho , AC= 5cm. Tính AB 4,2 c) Tìm x, y trên hình vẽ 62 = 3.x => x = 36 : 3 = 12 Áp dụng định lý Pitago, ta có : y2 = 62 + x2 = 62 + 122 = 36 + 144 = 180 => y = ≈ 13,4 Bài 2: (2 đ) Cho tam giác ABC vuông tại A , đường cao AH. Biết AH = 4, BH = 3. Tính tanB và số đo góc C . Ta có : tanB = (1 đ) B 5308’ => C 36052’ (0,5 đ). Bài 3 : (1 đ) Tính : = 2 Bài 4: (2đ) Cho tam giác ABC vuông tại A có Hình vẽ 0,25 đ a) Giải tam giác vuông ABC. Tính đúng góc C = 600 0,25 đ Ta có: ≈ 3,46 (cm) 0,25 đ ≈ 6,93 (cm) 0,25 đ b) Vẽ đường cao AH và trung tuyến AM của tam giác ABC. Tính diện tích tam giác AHM. Xét tam giác AHB, ta có : ≈ 5,2 (cm) HM = HB – MB = 3 – 2 = (cm) 0,5 đ Diện tích tam giác AHM: SAHM = = ≈ 2,6 cm2 0,5 đ ĐÁP ÁN ĐỀ 2 I. PHẦN TRẮC NGHIỆM KHÁCH QUAN (3 điểm) Mỗi câu đúng : 0,5 điểm Câu 1 2 3 4 5 6 Đáp án C B C B A A II. PHẦN TỰ LUẬN ( 7điểm) Bài HƯỚNG DẪN CHẤM Điểm 1 (2 đ) a) (sử dụng t/c tỉ số lượng giác của 2 góc phụ nhau để viết tg 830 = cotg 70 hoặc cotg70 = tg830) từ đó => tg830 – cotg 70 = 0 b) Biến đổi Biết tg+cotg = 3 ó từ đó suy ra 1, 0 điểm 0, 75 điểm 0, 25 điểm 2 (2 đ) Hình vẽ minh hoạ cho bài toán Gọi AB là chiều cao của tháp CA : hướng của tia nắng mặt trời chiếu xuống CB : bóng của tháp trên mặt đất (dài 96m). Trong tam giác ABC, B = 900. Ta có Hay AB = 96.1,1917 114,4 (m) 0,5 điểm 1điểm 0,5 điểm 3 (3 đ) Vẽ hình , ghi GT-KL đúng a) Sử dụng ĐL Pitago cho Δ vuông BHD tính được BD = 20cm Sử dụng ĐL Pitago cho Δ vuông BHC tính được HC = 9cm Tính DC2 + BC2 = 162 + 152 = 400 = DB2 => ΔBCD vuông tại B hay BD BC b) Kẻ AKDC tại K, tính được AB = KH = 7cm tính được SABCD = 192 cm2 c) SinBCD = BCD 36052’ 0,5 điểm 0,25 điểm 0,25 điểm 0,25 điểm 0, 5 điểm 0, 5 điểm 0,75 điểm HƯỚNG DẪN CHẤM MÔN TOÁN LỚP 9 đề 4 Câu 1 : nêu được cách dựng , vẽ hình đúng, chứng minh đúng 1đ Câu 2: vẽ hình, tính 0,5đ Tính 0,5đ Câu 3 : vẽ hình, tính 0,5đ Tính AC = AB.tan 60 = (cm) 0,5đ Câu 4 :sắp xếp đúng Cos80 < sin16<cos70<sin25<cos50<sin55 1đ Câu 5: vẽ hình và Tính BC = 20cm (dùng Pitago) 0,5đ .Tính SinB =12/20,CosB=.16/20 0,5đ Câu 6: 1đ Câu 7: tính đúng = 1 1đ Câu 8: vẽ hình và tính AC =15cm(dùng Pitago) 0,5đ Tính BC =25cm; AB= 20cm 0,5đ Câu 9: vẽ hình 0,25đ Tính AB =, Tính AC = 0,5đ => chu vi tam giác là AB+AC +BC = 6+8+10 =24cm 0,25đ Câu 10: vẽ hình 0,25đ Tính được AH=cm 0,25đ Chứng minh được AH=DE 0,25đ => DE =12cm 0,25đ Lưu ý: Học sinh không được dùng máy tính bỏ túi và bảng số. HƯỚNG DẪN CHẤM I. TRẮC NGHIỆM: Đúng mỗi câu 0,5 điểm Câu 1 2 3 4 5 6 Đáp án B D D B A C II. TỰ LUẬN. Bài 1: BC = 10 cm x = 3,6 y = 6,4 h = 4,8 1 1 Bài 2: AH = 10. sin 450 = 10.= 5 AB = AH: sin 300 = 5: = 10 0.75 0.75 Bài 3 Hình vẽ đúng: 0.5 a)AC2+ AB2 =25 BC2 = 25 AC2+ AB2 = BC2 Vậy tam giác ABC vuông tại A 0.5 0.5 b) AE là phân giác góc Â, nên: 0.25 0.25 0.25 0.25 c) Tứ giác AEDF có: Þ AEDFlà hình chữ nhật. 0.25 Có đường chéo AE là phân giác Â Þ AEDF là hình vuông ; 0.25 0.25 0.25 Đáp án : Đề 1 Câu Đáp án Điểm Bài 1 (3,5 đ) Bài 2 : ( 1 đ) Bài 3 (4,5 đ) 1,5đ (2,5đ) (1,5đ) 1đ a. x2 = 4.9 => x = 6 b. 4,2 cm c. Ta có : 62 = 3.x => x = 36 : 3 = 12 Áp dụng định lý Pitago, ta có : y2 = 62 + x2 = 62 + 122 = 36 + 144 = 180 y = ≈ 13,4 Tính : = (cos2200 + sin2200) + (cos2400 + sin2400) = 1 + 1 =2 Hình vẽ đúng 1/ Giải tam giác vuông ABC ABC vuông tại A, nên: CosB = Do đó: AC = BCsinB = 6sin600 = cm 2/Gọi E, F lần lượt là hình chiếu của H trên cạnh AB và AC: a/ Tính độ dài AH và chứng minh EF = AH AHB vuông tại H nên: AH = AB.sinB = 3.sin600 = cm Tứ giác AEHF có: (gt) Nên tứ giá AEHF là hình chữ nhật EF = AH b/ Tính: EAEB + AFFC Ta có: EAEB = HE2 ; AFFC = FH2 Nên EAEB + AFFC = HE2 + FH2 = EF2 Mà EF = AH (cmt) Do đó: EAEB + AFFC =AH2 = cm 1đ 1đ 1,5đ 1đ 0,5đ (Mỗi ý đúng cho 0,5đ) 0,5đ 0,5đ 0,5đ (0,5 đ) (0,5 đ) Bài 4 (1đ) Cho sin = . Hãy tính tan Ta có: sin2 + cos2 = 1 Cos2 = 1- sin2 = 1- = cos = Do đó: tan = (0,25đ) (0,25đ) (0,25đ) (0,25đ) Đáp án và biểu điểm ( đề 3 ) I/ Trắc nghiệm: (3 điểm) Mỗi câu đúng 0.5 điểm Câu 1 2 3 4 5 6 Đáp án B C D B D A II/ Tự luận: (7 điểm) Bài Ý Nội dung Điểm 1 2 Hình AC = AB.cotC = 30.cot300 = 30 (cm) 0.5 0.5 0.5 0.5 2 3 Hình 0.5 2.a 0.25 0.5 0.25 0.5 2.b 0.5 0.25 0.25 3 1 0.5 0.5 4 1 Vì AM là đường trung tuyến ứng với cạnh huyền nên: Trong tam giác vuông AMH có: . H:0,25 0,25 0,25 0,25 Trường THCS Trần Quang Khải KIỂM TRA 45’ Họ và tên:...................................... HÌNH HỌC 9 Lớp 9.......... MĐ1 ĐIỂM LỜI PHÊ I.TRẮC NGHIỆM: (3 điểm)Khoanh tròn trước chữ cái đáp án đúng Câu 1 : Tam giác nào sau đây là tam giác vuông , nếu độ dài 3 cạnh là : A. 11 cm ; 13 cm ; 6 cm B. 7 cm ; 8 cm ; 12 cm C. 6 cm ; 8 cm ; 10 cm D. 7cm ; 8cm; 10cm Câu 2 :Cho biết Sin = 0,1745 . Vậy số đo của góc (làm tròn đến phút) là : A. 1204’ B.1003’ C.12022’ D.9015’ Câu 3 :Tam giác ABC vuông tại A , có AC = 6 cm và BC = 12 cm . Vậy số đo của góc ACB là bao nhiêu ? (làm tròn đến độ) A. 450 B. 600 C. 300 D. 500 Câu 4 :Tam giác ABC có độ dài ba cạnh là AB = 3 cm ; AC = 4 cm ; BC = 5 cm . Độ dài đường cao AH là : (làm tròn đến 1 chữ số thập phân ). A. 4,8 cm B. 3,6 cm C. 2,4 cm D. 3cm Câu 5 : Cho tam giác IEF vuông tại I , đường cao IH . Câu nào sau đây sai ? A. IF2 = HF.EF B. IH2 = IE.EF C. D. IE.IF = IH.EF Câu 6 : Biết A. 450 B. 600 C. 300 D. 900 II. BÀI TẬP TỰ LUẬN : (7 điểm) Bài 1 : (1,5 điểm) Tính x, y trên hình vẽ Bài 2 : (1,5 điểm) Bóng của một cột điện trên mặt đất dài 25 m, tia nắng mặt trời tạo với mặt đất một góc bằng 300. Tính chiều cao cột điện (làm tròn đến chữ số thập phân thứ 2 ). Bài 3 : (3 điểm) Cho tam giác ABC có độ dài ba cạnh là AB = 20 cm , AC = 21 cm , BC = 29 cm Chứng minh tam giác ABC vuông tại A . Tính góc B , góc C . Kẻ đường cao AH của tam giác ABC . Tính chiều cao AH và các đoạn mà chiều cao đó chia ra trên cạnh BC . (làm tròn đến chữ số thập phân thứ 2 ). Bài 4 : (1điểm) a)Không dùng bảng số và máy tính , hãy tính : A = Cos2150 + Cos2250 + Cos2350 + Cos2550 + Cos2650 + Cos2750 – 3 . b) Cho . Tính giá trị của biểu thức A = BIỂU ĐIỂM VÀ ĐÁP ÁN : I.TRẮC NGHIỆM: (3 điểm) Mỗi câu 0,5 điểm . Câu 1: (C) Câu 2: (B) Câu 3: (B) Câu 4: (A) Câu 5: (B) Câu 6: (B) II. BÀI TẬP TỰ LUẬN : (7 điểm) Bài 1: Dựng góc vuông xOy . lấy một đoạn thẳng làm đơn vị . Trên tia Ox lấy điểm A sao cho OA = 2 ; trên tia Oy , lấy điểm B sao cho OB = 3 . Góc OBA bằng góc cần dựng 0,5 điểm Thật vậy ta có : Tg = tgOBA = Hình 0,5 điểm Bài 2 : (2 điểm) Chiều cao cột điện : Bài 3 : AB2 + AC2 = 202 + 212 = 400 + 441 = 841 0,5 điểm BC2 = 292 = 841 Do đó : BC2 = AB2 + AC2 Vậy tam giác ABC vuông tại A 0,5 điểm Bài 4 : A = (Sin2150 + Cos2150) + (Sin2250 + Cos2250) + (Sin2350 + Cos2350) – 3 0,5 điểm A = 1 + 1 + 1 – 3 0,5 điểm A = 0 Trường THCS Trần Quang Khải KIỂM TRA 45’ Họ và tên:...................................... HÌNH HỌC 9 Lớp 9.......... MĐ2 ĐIỂM LỜI PHÊ I.TRẮC NGHIỆM: (3 điểm)Khoanh tròn trước chữ cái đáp án đúng Câu 1: Dựa vào hình 1. Hãy chọn câu đúng: A) BA2 = BC. CH B) BA2 = BC. BH C) BA2 = BC2 + AC2 D) AH.AB = AC.BC Câu 2: Dựa vào hình 1. Độ dài của đoạn thẳng AH bằng: A) AB.AC B) BC.HB C) D) BC.HC Câu 3: Dựa vào hình 1. Hãy chọn câu đúng: A) B) C) D) Câu 4: Hãy chọn câu đúng: A) sin370 = sin530 B) cos370 = sin530 C) tan370 = cot370 D) cot370 = cot530 Câu 5: Cho DABC vuông tại A. Câu nào sau đây đúng và đầy đủ nhất ? A) AC = BC.sinC B) AB = BC.cosC C) AC = BC.sinB D) AC = AB.sinC Câu 6 Cho DABC vuông tại A, biết AB = 3cm, AC = 4cm, BC = 5cm. Hãy chọn đáp đúng A) cosB= B) sinB= C) tanB= D) cotB= II.PHẦN TỰ LUẬN: (7.0 điểm) Bài 1 : (1,5 điểm) Tính x, y trên hình vẽ Bài 2: (1,5 điểm) Cho DABC vuông tại A, có AB = 30cm, và C = 300. Giải tam giác vuông ABC. Bài 3: (3 điểm) Cho DABC vuông tại A, đường cao AH. Biết HB = 3,6cm ; HC = 6,4cm. Tính độ dài các đoạn thẳng: AB, AC, AH. Kẻ HEAB ; HFAC. Chứng minh rằng: AB.AE = AC.AF. Bài 4: ( 1 điểm) a)Không dùng bảng số và máy tính , hãy tính : b) Rút gọn biểu thức:
Tài liệu đính kèm:
 bo_10_de_on_tap_chuong_i_mon_hinh_hoc_lop_9_co_dap_an.doc
bo_10_de_on_tap_chuong_i_mon_hinh_hoc_lop_9_co_dap_an.doc



