Đề cương ôn tập chương III môn Đại số Lớp 9

ÔN TẬP CHƯƠNG III ĐẠI SỐ 9
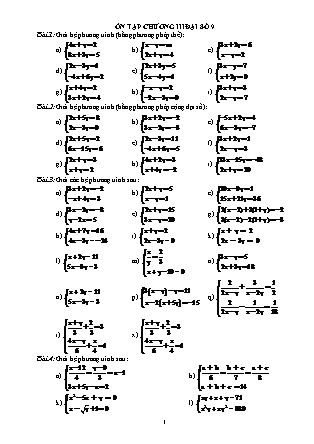
Bài 1: Giải hệ phương trình (bằng phương pháp thế):
 	a) 	 	b) 	c) 	
d) 	e) 	 	f) 	
g) 	h) 	i) 
Bài 2: Giải hệ phương trình (bằng phương pháp cộng đại số):
 	a) 	b) 	c) 	
d) 	e) 	 	f) 	
g) 	h) 	i) 
Bài 3: Giải các hệ phương trình sau:
 	a) 	b) 	c) 	
d) 	e) 	g) 	
h) 	i) 	k) 	
l) 	m) 	n) 
o) 	p) 	q) 	
r) 	x) 
Bài 4: Giải hệ phương trình sau: 
a) 	b) 
k) 	l) 
c) 	d) 
e) 	f) 
h) 	i) 	
Bài 5: Đặt ẩn phụ rồi giải các hệ phương trình sau: 
a) 	b) 
Bài 6: Giải các hệ phương trình sau:
 	a) 	b) 	
Bài 7: Xác định a ; b để hệ phương trình có nghiệm là x = 3 ; y = –1 
Bài 8: Tìm m để hệ phương trình sau có vô số nghiệm: 
Bài 9: Tìm nghiệm nguyên dương của phương trình: xy – 2x + 3y = 27.
Bài 10: Cho hệ phương trình: 
 	a) Tìm m, n để hệ phương trình có nghiệm: (x ; y) = (–2 ; 3)
 	b) Tìm m, n để hệ phương trình có vô số nghiệm.
Bài 11: Cho hpt: . Tìm m để hpt có nghiệm thỏa mãn x > 0 ; y < 0.
Bài 12: Tìm các hệ số a và b biết hpt: có nghiệm (x ; y) = (3 ; 1) 
Bài 13: Cho hệ phương trình: 
 Xác định m để hệ phương trình có một nghiệm? Vô nghiệm? Vô số nghiệm?
Bài 14: Tìm giá trị của m để hệ phương trình Vô nghiệm? vô số nghiệm?
Bài 15: Cho hệ phương trình: (I)
 	a) Giải hệ phương trình (I)
 	b) Tìm m để x, y là số nguyên.
Bài 16: Cho hệ phương trình: 
 	a) Tìm m để hệ có nghiệm duy nhất thỏa mãn x + y = –1.
 	b) Tìm m nguyên để hệ có nghiệm duy nhất là nghiệm nguyên.
Bài 17: Viết phương trình đường thẳng (d) đi qua 2 điểm:
 	a) (2 ; 1) và (–1 ; –5)	b) (4 ; –1) và (3 ; 2)
Bài 18: Cho ba điểm: A(2 ; 1) ; B(–1 ; –2) ; C(0 ; –1)
 	a) Viết phương trình đường thẳng AB
 	b) Chứng minh ba điểm A, B, C thẳng hàng.
 	c) Tìm a và b để (d): y = (2a – b)x + 3a – 1 đi qua điểm B và C.
Bài 19: Chứng minh các đường thẳng sau, luôn đi qua một điểm cố định khi m thay đổi
 	(d): mx – y = 3m + 2	(d): 2 mx + y = (3m – 2) – 2x
 	(d): y = 3mx + m + 2	(d): (m – 3)x – 3y = m + 2010	
Bài 20: Cho f(x) = x2 + bx + c. Tìm b và c biết
 	a) f(1) = 2 ; f(–3) = 0
 	b) f(x) có nghiệm là 3 ; –6. 
Bài 21: Tìm các giá trị của m để ba đường thẳng sau đồng quy tại một điểm trong mặt phẳng tọa độ:
 	a) 3x + 2y = 5 ; 2x – y = 4 và mx + 7y = 11
 	b) y = 2x + 3 ; y = x + 4 ; y = (3 – 5m)x – 5m
 	c) 3x + y = 5 ; 2x + y = –4 và (4m – 1)x + y = –1
Bài 22: Tìm m và n để (d): y = (2b – a) x – 3(a + 5b), đi qua hai điểm:
 	a) (2 ; 4) ; (–1 ; 3)
 	b) (2 ; 1) ; (1 ; –2) 
Bài 23: Cho các đường thẳng:	y = x – 2 (d1)
 	y = 2x – 4 (d2)
	y = mx + (m + 2) (d3)
 	a) Tìm điểm cố định mà đường thẳng (d3 ) luôn đi qua với mọi giá trị của m.
 	b) Tìm m để ba đường thẳng (d1) ; (d2) ; (d3) đồng quy.
Bài 24: Xác định a, b để đường thẳng y = ax + b đi qua hai điểm:
 	a) A(–1 ; 3) và B(–1 ; –4)
 	b) M(1 ; 2) và N(–1 ; –4)
Bài 25:
 	a) Cho A(2 ; 4) và B(5 ; 2). Tìm trên trục hoành điểm M sao cho tổng khoảng cách từ M tới A và B là nhỏ nhất.
 	b) Cho A(–6 ; –2) và B (–3 ; –4). Tìm trên trục hoành điểm M sao cho tổng khoảng cách từ M tới A và B là nhỏ nhất.
Bài 26: Biết hai số tự nhiên m và p thoả mãn 
 	a) Tính m + p.
 	b) Tính m và p.
Bài 27: Tìm a và b biết rằng phương trình ax2 – 2bx + 3 = 0 có tập nghiệm S = {–2 ; 1}
Bài 28: Một ca nô dự định đi từ A đến B trong thời gian đã định. Nếu ca nô tăng 3 km/h thì đến nơi sớm 2 giờ. Nếu ca nô giảm vận tốc 3 km/h thì đến nơi chậm 3 giờ. Tính chiều dài khúc sông AB. 
Bài 29: Một hình chữ nhật có chu vi 110m. Hai lần chiều dài hơn ba lần chiều rộng là 10m. Tính diện tích hình chữ nhật.
Bài 30: Một người đi xe đạp đự định đi hết quãng đường AB với vận tốc 10 km/h. Sau khi đi dược nửa quãng đường với vận tốc dự định người ấy nghỉ 30 phút. Vì muốn đến được điểm B kịp giờ nên người với vận tốc 15 km/h trên quãng đường còn lại. Tính quãng đường AB.
Bài 31: Hai người cùng làm một công việc trong 7 giờ 12 phút thì xong công việc. Nếu người thứ nhất làm trong 4 giờ người thứ hai làm trong 3 giờ thì đựơc 50% công việc. Hỏi mỗi người làm một mình trong mấy giờ thì xong công việc ?
Bài 32: Một đoàn xe vận tải có 15 xe tải lớn và 4 xe tải nhỏ tất cả chở 178 tấn hàng. Biết mỗi xe tải lớn chở nhiều hơn xe tải nhỏ là 3 tấn. Tính số tấn hàng mỗi xe tải từng loại đã chở ? 
Bài 33: Một ôtô đi từ A đến B với vận tốc và thời gian đã định. Nếu vận tốc ôtô tăng thêm 10 km/h thì đến B sớm hơn 30 phút so với dự định. Nếu vận tốc ôtô giảm đi 5 km/h thì đến B muộn 20 phút so với dự định. Tìm quãng đường AB.
Bài 34: Một mảnh đất hình chữ nhật có chu vi là 90m. Nếu giảm chiều dài 5m và chiều rộng 2m thì diện tích giảm 140m2. Tính diện tích mảnh đất đó.
Bài 35: Có hai ôtô khởi hành cùng 1 lúc từ 2 tỉnh A và B cách nhau 35 km. Nếu đi ngược chiều 2 xe gặp nhau sau 5 giờ. Tìm vận tốc mỗi xe, biết rằng xe đi từ A đi nhanh hơn xe kia 10 km mỗi giờ.
Bài 36: Trong một trang sách, nếu bớt đi 5 dòng và mỗi dòng bớt đi 2 chữ thì cả trang sách sẽ bớt đi 150 chữ. Nếu tăng thêm 6 dòng và mỗi dòng thêm 3 chữ thì cả trang sách sẽ tăng thêm 228 chữ. Tính số dòng trong trang sách và số chữ trong mỗi dòng.
Bài 37: Một ô tô và một mô tô khởi hành cùng một lúc từ hai địa điểm A và B cách nhau 200 km đi ngược chiều và gặp nhau sau 2,5 giờ. Tính vận tốc của ôtô và mô tô, biết rằng vận tốc mô tô nhỏ hơn vận tốc ôtô là 20 km/h.
Bài 38: Một ôtô đi trên đoạn đường AB với vận tốc 55 km/h, rồi tiếp tục từ B đến C với vận tốc tăng thêm 5 km/h. Biết quãng đường tổng cộng dài 290 km và thời gian ôtô đi trên đoạn đường AB ít hơn thời gian ôtô đi trên đoạn đường BC là 1 giờ. Tính thời gian ôtô đi trên mỗi đoạn đường AB và BC.
Bài 39: Tìm hai số biết tổng của chúng bằng 7 và tổng nghịch đảo bằng ?
Bài 40: Một canô xuôi dòng 108 km, rồi ngược dòng 63 km, mất 7 giờ. Lần thứ hai, canô đó xuôi dòng 81 km rồi ngược dòng 84 km cũng mất 7 giờ. Tính vận tốc dòng nước, vận tốc thực của canô.
Bài 41: Hai tổ cùng làm một công việc. Nếu làm riêng một mình thì tổ A cần 20 giờ, tổ B cần 15 giờ mới làm xong. Người ta giao cho tổ A làm trong một thời gian rồi nghỉ và tổ B làm tiếp cho xong. Biết thời gian tổ A làm ít hơn tổ B là 3 giờ 20 phút. Tính thời gian mỗi tổ đã làm.
Bài 42: Một tổ dệt khăn mặt, mỗi ngày theo kế hoạch phải dệt 500 chiếc, nhưng thực tế mỗi ngày đã dệt thêm được 60 chiếc, cho nên chẳng những đã hoàn thành kế hoạch trước 3 ngày mà còn dệt thêm được 1200 khăn mặt so với kế hoạch. Tìm số khăn mặt phải dệt theo kế hoạch lúc đầu.
Bài 43: Một máy bơm muốn bơm đầy nước vào một bể chứa trong 1 thời gian quy định thì mỗi giờ phải bơm 10m3. Sau khi bơm được dung tích của bể chứa, người công nhân vận hành cho máy bơm với công suất lớn hơn, mỗi giờ bơm được 15m3 do đó bể được bơm đầy trước 48 phút so với thời gian quy định. Tính dung tích bể chứa.
Bài 44: Hai cạnh góc vuông của một tam giác vuông hơn kém nhau 2 cm. Nếu giảm cạnh lớn đi 4 cm và tăng cạnh nhỏ lên 6 cm thì diện tích không đổi. Tính diện tích của tam giác vuông.
Bài 45: Hai ca nô cùng khởi hành từ hai bến A và B cách nhau 170 km và đi ngược chiều nhau. Sau 3 giờ 20 phút thì hai ca nô gặp nhau. Tính vận tốc riêng của mỗi ca nô, biết vận tốc ca nô xuôi dòng lớn hơn vận tốc của ca nô đi ngược dòng là 9 km/h và vận tốc dòng nước là 3km/h.
Bài 46: Hai vòi nước cùng chảy vào bể không có nước thì sau 5 giờ đầy bể. Nếu mở vòi thứ nhất chảy trong 6 giờ và vòi thứ hai chảy trong 2 giờ thì đợc bể nước. Hỏi nếu mỗi vòi chảy một mình thì sau bao lâu sẽ đầy bể ?
Bài 47: Một ôtô đi từ Hà Nội đến Thanh Hoá với một vận tốc và thời gian đã định. Nếu vận tốc ôtô giảm 10 km/h thì thời gian tăng 45 phút. Nếu vận tốc ôtô tăng 10 km/h thì thời gian giảm 30 phút. Tính vận tốc và thời gian đã định của ôtô. Quãng đường Hà Nội – Thanh Hoá là bao nhiêu ?
Bài 48: Tìm hai số tự nhiên mà tổng của chúng bằng 168 và ước chung lớn nhất của chúng bằng 24.
Bài 49: Có thể đổi một đồng tiền loại 100 000 đồng thành 30 đồng tiền loại 5 000 đồng và 1 000 đồng không ?
Bài 50: Hai người làm chung một công việc thì sau 20 ngày sẽ hoàn thành. Nhng sau khi làm chung được 10 ngày thì người thứ nhất đi làm việc khác, người thứ hai vẫn tiếp tục công việc đó và hoàn thành trong 15 ngày. Hỏi nếu làm riêng thì mỗi người phải làm trong bao nhiêu ngày để hoàn thành công việc.