Đề cương ôn tập thi giữa kỳ I môn Toán Lớp 9
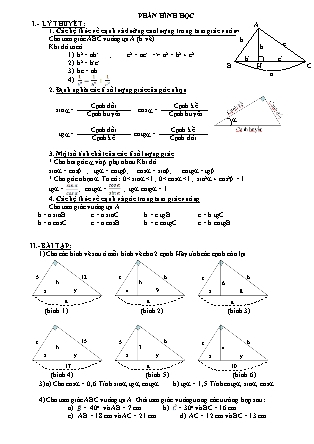
6) Cho ABC vuông tại A. Biết AB = 7cm và AC = 21cm.
Tính các tỉ số lượng giác của góc B và C.
7) Cho tam giác ABC có AB = 6cm, AC = 4,5cm, BC = 7,5cm.
a) Chứng minh tam giác ABC vuông tại A.
b) Tính các góc B, C và đường cao AH của tam giác.
c) Tính diện tích của tam giác ABC.
8) Cho tam giác ABC vuông tại A, đường cao AH chia cạnh huyền BC thành hai đoạn BH và CH lần lượt có độ dài là 4cm và 9cm. Gọi D và E lần lượt là hình chiếu của H trên AB và AC.
a) Tính độ dài đoạn thẳng DE.
b) Các đường thẳng vuông góc với DE tại D và E lần lượt cắt BC tại M và N.
Chứng minh M là trung điểm của BH và N là trung điểm của CH.
c) Tính diện tích của tứ giác DEMN.
9) Cho tam giác ABC vuông tại A, AB = 15cm, AC = 20cm.
a) Tính BC, B, C.
b) Phân giác của góc A cắt BC tại E. Tính BE, CE.
c) Từ E kẻ EM và EN lần lượt vuông góc với AB và AC. Hỏi tứ giác AMEN là hình gì? Tính chu vi và diện tích của tứ giác AMEN
10) Cho hình thang ABCD (AB // CD ). Vẽ BH ^ CD (H thuộc CD) .
Cho biết BH = 12cm , DH = 16cm, CH = 9 cm , AD = 14cm.
a) Tính độ dài DB , BC .
b) Chứng minh tam giác DBC vuông
c) Tính các góc của hình thang ABCD (làm tròn đến độ)
12) Cho tam giác nhọn ABC và các đường cao BD và CE . Trên CE lấy điểm M sao cho góc AMC = 900, trên BD lấy điểm N sao cho góc ANB = 900. Chứng minh tam giác AMN cân.
PHẦNA B C b/ c/ H b c a h HÌNH HỌC I.- LÝ THUYẾT: 1. Các hệ thức về cạnh và đường cao lượng trong tam giác vuông Cho tam giác ABC vuông tại A (h.vẽ) Khi đó ta có 1) b2 = ab/ ; c2 = ac/ => a2 = b2 + c2 2) h2 = b/c/ 3) bc = ah 4) 2. Định nghĩa các tỉ số lượng giác của góc nhọn sina = Cạnh đối cosa = Cạnh kề Cạnh huyền Cạnh huyền tga = Cạnh đối cotga = Cạnh kề Cạnh kề Cạnh đối a 3. Một số tính chất của các tỉ số lượng giác * Cho hai góc a và b phụ nhau. Khi đó sina = cosb ; tga = cotgb; cosa = sinb; cotga = tgb * Cho góc nhọn a. Ta có: 0< sina <1 ; 0< cosa <1 ; sin2a + cos2b = 1 tga = ; cotga = ; tga.cotga = 1 4. Các hệ thức về cạnh và góc trong tam giác vuông Cho tam giác vuông tại A. b = a.sinB c = a.sinC b = c.tgB c = b.tgC b = a.cosC c = a.cosB b = c.cotgC c = b.cotgB II.- BÀI TẬP: 1) Cho các hình vẽ sau ở mỗi hình vẽ cho 2 cạnh. Hãy tính các cạnh còn lại. 5 12 x y a h c b 4 9 a h c b x 8 a 6 (hình 1) (hình 2) (hình 3) c 15 x y 17 h 5 b x y a 3 c b x y 10 4 (hình 4) (hình 5) (hình 6) 3) a) Cho cosa = 0,6. Tính sina, tga, cotga. b) tga = 1,5. Tính cotga, sina, cosa. 4) Cho tam giác ABC vuông tại A. Giải tam giác vuông trong các trường hợp sau: a) = 400 và AB = 7 cm b) = 300 và BC = 16 cm. c) AB = 18 cm và AC = 21 cm d) AC = 12 cm và BC = 13 cm 5) Cho tam giác ABC, = 400, = 300, đường cao AH = 6cm . Tính AB, AC và BC. 6) Cho ABC vuông tại A. Biết AB = 7cm và AC = 21cm. Tính các tỉ số lượng giác của góc B và C. 7) Cho tam giác ABC có AB = 6cm, AC = 4,5cm, BC = 7,5cm. a) Chứng minh tam giác ABC vuông tại A. b) Tính các góc B, C và đường cao AH của tam giác. c) Tính diện tích của tam giác ABC. 8) Cho tam giác ABC vuông tại A, đường cao AH chia cạnh huyền BC thành hai đoạn BH và CH lần lượt có độ dài là 4cm và 9cm. Gọi D và E lần lượt là hình chiếu của H trên AB và AC. a) Tính độ dài đoạn thẳng DE. b) Các đường thẳng vuông góc với DE tại D và E lần lượt cắt BC tại M và N. Chứng minh M là trung điểm của BH và N là trung điểm của CH. c) Tính diện tích của tứ giác DEMN. 9) Cho tam giác ABC vuông tại A, AB = 15cm, AC = 20cm. a) Tính BC, B, C. b) Phân giác của góc A cắt BC tại E. Tính BE, CE. c) Từ E kẻ EM và EN lần lượt vuông góc với AB và AC. Hỏi tứ giác AMEN là hình gì? Tính chu vi và diện tích của tứ giác AMEN 10) Cho hình thang ABCD (AB // CD ). Vẽ BH ^ CD (H thuộc CD) . Cho biết BH = 12cm , DH = 16cm, CH = 9 cm , AD = 14cm. a) Tính độ dài DB , BC . b) Chứng minh tam giác DBC vuông c) Tính các góc của hình thang ABCD (làm tròn đến độ) 12) Cho tam giác nhọn ABC và các đường cao BD và CE . Trên CE lấy điểm M sao cho góc AMC = 900, trên BD lấy điểm N sao cho góc ANB = 900. Chứng minh tam giác AMN cân. ĐỀ 1 : Câu 1: ( 2đ) Cho hình vẽ 1 . Hãy tính các tỉ số lượng giác của góc B. Hình vẽ 1 Câu 2: ( 2đ) Tìm x; y trên hình vẽ 2. Hình vẽ 2 Câu 3: ( 1 đ) Tính : Câu 4: (5đ) Cho tam giác ABC vuông tại A có a) Giải tam giác vuông ABC. b) Vẽ đường cao AH và trung tuyến AM của tam giác ABC. Tính diện tích AHM. c) Xác định số đo của để ( Kết quả Số làm tròn đến 2 chữ số thập phân, góc làm tròn đến phút ) ĐỀ 2 : Bài 1: (5 điểm). Cho tam giác ABC vuông tại A, đường cao AH, AB = 3cm, BC = 6cm. a) Giải tam giác vuông ABC b) Gọi E, F lần lượt là hình chiếu của H trên cạnh AB và AC: 1. Tính độ dài AH và chứng minh: EF = AH. 2. Tính: EAEB + AFFC Bài 2: (2 điểm). Cho sin = 0,6. Hãy tính cos; tan; Bài 3 : ( 1 điểm ) Tính : Bài 4 : (2 điểm). Cho tam giác DEF có ED = 7cm; = 400; = 580 . Kẻ đường cao EI của tam giác đó. Hãy tính: (Kết quả làm tròn đến chữ số thập phân thứ 1) Đường cao EI Cạnh EF Chứng minh: SDEF = DE.DF. sinD PHẦN ĐẠI SỐ ĐỀ 1: Bài 1: Rút gọn biểu thức: - Bài 2: Giải phương trình: = 2 Bài 3: Chứng minh đẳng thức = 4 Bài 4: Cho biểu thức P = (với x>0 và x) Rút gọn P. b) Tìm x để P ĐỀ 2: Bài 1: Rút gọn biểu thức: + Bài 2: Giải phương trình: = 4 Bài 4: Cho biểu thức Q = (với x>0 và x) Rút gọn Q. b) Tính giá trị của Q khi x = 9 Bài 5: Chứng minh đẳng thức ĐỀ 3: Bài 1: a) Tìm điều kiện để căn thức bậc hai có nghĩa b) Bài 2: Rút gọn biểu thức: a) b) + c) d) Bài 3: Giải phương trình: = 2 Bài 4: Cho biểu thức P = a) Tìm điều kiện của x để biểu thức P xác định. b) Rút gọn P c) Tìm các giá trị của x để P < 0 Bài 5: Cho Q = . Tìm giá trị lớn nhất của Q. ĐỀ 4: Bài 1: a) Tìm điều kiện để căn thức bậc hai có nghĩa b) Bài 2: Rút gọn biểu thức: a) b) c) Bài 3: Giải phương trình: a/ b/ Bài 4: Cho biểu thức: (với) a) Rút gọn biểu thức A. b) Tính giá trị của x khi A Bài 5: Chứng minh đẳng thức: = 2 ĐỀ 5: Bài 1: a) Tìm điều kiện để căn thức bậc hai có nghĩa b) Bài 2: Rút gọn biểu thức: a) b) c) d) Bài 3: Giải phương trình: a/ b/ Bài 4: Cho biểu thức: (với) a) Rút gọn biểu thức A. b) Tính giá trị nhỏ nhất của A Bài 5: Chứng minh với ; ĐỀ 6: Bài 1: a) Tìm điều kiện để căn thức bậc hai có nghĩa b) Bài 2: Rút gọn biểu thức: a) b) c) Bài 3: Giải phương trình: a/ b/ Bài 4: Cho biểu thức: (với) a) Rút gọn biểu thức P. b) Tính giá trị của P khi a = Bài 5: Chứng minh đẳng thức ĐỀ 7: (KT 2018-2017) Bài 1: (1,0 đ) Tìm điều kiện để căn thức bậc hai có nghĩa. a) b) Bài 2: (2,0 đ) Thực hiện phép tính: a) b) Bài 3: (4,0 đ) Rút gọn các biểu thức: a) b) c) d) Bài 4: (1,5 đ) Giải phương trình: Bài54: (1,5 điểm) Cho biểu thức: (với) a) Rút gọn biểu thức A. b) Tính giá trị của A khi a = . Bài 6: (0,5 điểm) Chứng minh đẳng thức: ĐỀ 8: Bài 1: (1,0 đ) Tìm điều kiện để căn thức bậc hai có nghĩa. a) b) Bài 2: (4,0 đ) Rút gọn các biểu thức: a) b) c) d) Bài 3: (2,5 đ) Giải phương trình: a) b) Bài 4: (2,0 điểm) Cho biểu thức: (với) a) Rút gọn biểu thức A. b) Tính giá trị của x khi A =. Bài 5: (0,5 điểm) Chứng minh đẳng thức:
Tài liệu đính kèm:
 de_cuong_on_tap_thi_giua_ky_i_mon_toan_lop_9.doc
de_cuong_on_tap_thi_giua_ky_i_mon_toan_lop_9.doc



