Đề kiểm tra giữa học kỳ I môn Toán Lớp 9 - Năm học 2020-2021 - Trường THCS Võ Xán (có đáp án)

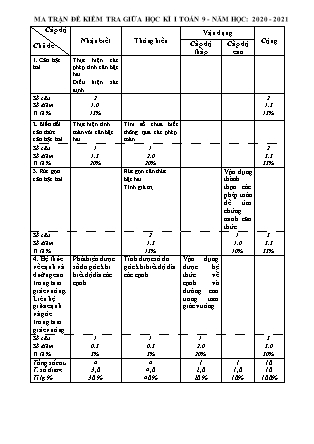
MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KÌ I TOÁN 9 - NĂM HỌC: 2020 - 2021
 Cấp độ
Chủ đề 
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
1. Căn bậc hai
Thực hiện các phép tính căn bậc hai.
Điều kiện xác định
Số câu 
Số điểm 
Tỉ lệ %
2
1,0
15%
2
1,5
15%
2. Biến đổi căn thức căn bậc hai
Thực hiện tính toán với căn bậc hai
Tìm số chưa biết thông qua các phép toán
Số câu 
Số điểm 
Tỉ lệ %
1
1,5
20%
1
2,0
20%
2
3,5
35%
3. Rút gọn căn bậc hai
Rút gọn căn thức bậc hai.
Tính giá trị
Vận dụng thành thạo các phép toán để tìm chứng minh căn thức
Số câu 
Số điểm 
Tỉ lệ %
2
1,5
15%
1
1,0
10%
3
3,5
35%
4. Hệ thức về cạnh và đường cao trong tam giác vuông.
Liên hệ giữa cạnh và góc trong tam giác vuông
Phát hiện được số đo góc khi biết độ dài các cạnh.
Tính được số đo góc khi biết độ dài các cạnh
Vận dụng được hệ thức về cạnh và đường cao trong tam giác vuông.
Số câu 
Số điểm 
Tỉ lệ %
1
0,5
5%
1
0,5
5%
1
2,0
20%
3
3,0
30%
Tổng số câu 
T. số điểm
Tỉ lệ %
4
3,0
30 %
4
4,0
40 %
1
2,0
20 %
1
1,0
10%
10
10 
100%
PHÒNG GD&ĐT HUYỆN TÂY SƠN
TRƯỜNG THCS VÕ XÁN
ĐỀ KIỂM TRA GIỮA HỌC KỲ I – TOÁN 9
NĂM HỌC: 2020 – 2021
Thời gian: 90 phút
(Không kể thời gian phát đề)
Điểm
Lời nhận xét của giáo viên
ĐỀ BÀI:
Bài 1. (2,0 điểm). Thực hiện phép tính.
	a) 	b) 	
Bài 2. (2,0 điểm). Giải các phương trình sau:
	a) 	b) 
Bài 3. (2,0 điểm). Cho biểu thức 
	a) Tìm điều kiện xác định của A? 
b) Rút gọn biểu thức A. 
c) Tìm x để A = .
Bài 4. (3,0 điểm) Cho ABC vuông tại A., đường cao AH. Biết BH = 1.8 cm; HC = 3,2 cm.
a. Tính độ dài AH ; AB; AC.
b. Tính số đo góc B và góc C.
c. Tia phân giác của góc B cắt AC tại D. Tính độ dài BD.
d. Chứng mimh rằng: 
(số đo góc làm tròn đến độ, độ dài đoạn thẳng làm tròn đến chữ số thập phân thứ ba)
Bài 5. (1,0 điểm) Chứng minh đẳng thức sau: 
 với 
BÀI LÀM
ĐÁP ÁN VÀ THANG ĐIỂM
Câu hỏi
Đáp án
Điểm
Bài 1: 
(2,0 điểm)
a) 
1,0đ
b) 
1,0đ
Bài 2:
(2,0 điểm)
a) ĐK: 
 (T/m ĐKXĐ)
 Vậy phương trình có nghiệm duy nhất x = 24
1,0đ
b) 
Vậy không tìm được x thỏa điều kiện đề bài cho.
1,0đ
Bài 3:
(2,0 điểm)
ĐKXĐ: 
0,25đ
Với ta có 
Vậy A(với x > 0; x ¹ 1)
0,25đ
0,25đ
0,25đ
 (ĐK: x > 0 ; x ¹ 1)
 (TMĐK)
Vậy với x = 9 thì .
0,25đ
0,25đ
0,25đ
0,25đ
Bài 4:
(3,0 điểm)
0,25đ
a . Tính độ dài AH ; AB; AC.
 ABC có: , AH BC (gt )
Theo hệ thức về cạnh và đường cao trong tam giác vuông ta có:
 	AH2 = BH . HC = 1,8 . 3.2 = 5,76	
 AH = 	
AHB vuông tại H theo định lí py ta go :
 AB = 	
AHC vuông tại H theo định lí py ta go: 
AC = 
0,25đ
0,25đ
0,25đ
0,25đ
b . Tính góc B, C. 
Theo định nghĩa tỉ số lượng giác của góc nhọn ta có : 
 tan B = 
 nên = 900 
0,25đ
0,25đ
c. Tính BD 
 ABD () , 
Theo hệ thức về cạnh và góc trong tam giác vuông ta có: 
0,25đ
0,25đ
d. ABD vuông tại A ta có :
tan = (1)( định nghĩa tỉ số lượng giác
Ta lại có: BD là phân giác trong của ABC 
Nên (Tính chất đường phân giác)
==(2)
Từ (1) và (2) tan = 
0,25đ 
0,25đ
0,25đ
Bài 5:
(1,0 điểm)
Ta có:
 (đpcm)	 	
0,5đ
0,5đ
Lưu ý: 
Trên đây là các bước giải cơ bản cho từng bài, từng ý và biểu điểm tương ứng, học sinh phải có lời giải chặt chẽ chính xác mới công nhận cho điểm.
Học sinh có cách giải khác đúng đến đâu cho điểm thành phần đến đó.
Điểm toàn bài là tổng điểm thành phần không làm tròn.
Hết!